
分析 (1)由已知可知数列为公差是4的等差数列,再由a1+a4=14求得首项,可得等差数列的通项公式和前n项和;
(2)把等差数列的前n项和代入bn=$\frac{{S}_{n}}{n+k}$( k∈Z),由{bn}是等差数列求得k,得到{bn}的通项公式,利用裂项相消法求得{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn,由数列的函数特性求出Tn$<\frac{1}{2}$,结合Tn≤$\frac{m}{100}$恒成立求得正整数m的最小值.
解答 解:(1)由an+1=an+4,得an+1-an=4,可知数列{an}是公差为4的等差数列,
则a1+a4=2a1+3d=2a1+12=14,得a1=1.
∴an=1+4(n-1)=4n-3,${S}_{n}=n+\frac{4n(n-1)}{2}=2{n}^{2}-n$;
(2)bn=$\frac{{S}_{n}}{n+k}$=$\frac{2{n}^{2}-n}{n+k}$,∵{bn}是等差数列,
∴2b2=b1+b3,即$2×\frac{6}{2+k}=\frac{1}{1+k}+\frac{15}{3+k}$,解得k=0.
∴bn=2n-1.
则${T}_{n}=\frac{1}{{b}_{1}{b}_{2}}+\frac{1}{{b}_{2}{b}_{3}}+…+\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{1×3}+\frac{1}{3×5}+…+\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$(1$-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}$+…+$\frac{1}{2n-1}-\frac{1}{2n+1}$)=$\frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}$.
函数f(n)=$\frac{n}{2n+1}=\frac{1}{2+\frac{1}{n}}$在n>0时为增函数,且当n→+∞时,f(n)→$\frac{1}{2}$.
∴${T}_{n}<\frac{1}{2}$,由Tn≤$\frac{m}{100}$,得$\frac{m}{100}≥\frac{1}{2}$,得m≥50.
∴m的最小值为50.
点评 本题考查数列递推式,考查了裂项相消法求数列的和,训练了恒成立问题的求解方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
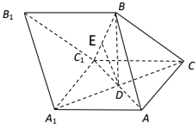 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16:9 | B. | 9:16 | C. | 27:8 | D. | 8:27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com