
| A. | (-∞,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{2}$,+∞) |
分析 f(x)=xlnx-2ax2(x>0),f′(x)=lnx+1-4ax.令g(x)=lnx+1-4ax,由于函数f(x)=x(lnx-2ax)有两个极值点?g(x)=0在区间(0,+∞)上有两个实数根.g′(x)=$\frac{1}{x}$-4a.当a≤0时,直接验证;当a>0时,利用导数研究函数g(x)的单调性可得:当x=$\frac{1}{4a}$时,函数g(x)取得极大值,故要使g(x)有两个不同解,只需要g($\frac{1}{4a}$)=ln$\frac{1}{4a}$>0,解得即可.
解答 解:f(x)=xlnx-2ax2(x>0),f′(x)=lnx+1-4ax.
令g(x)=lnx+1-4ax,
∵函数f(x)=x(lnx-ax)有两个极值点,
则g(x)=0在区间(0,+∞)上有两个实数根.
g′(x)=$\frac{1}{x}$-4a=$\frac{1-4ax}{x}$,
当a≤0时,g′(x)>0,则函数g(x)在区间(0,+∞)单调递增,
因此g(x)=0在区间(0,+∞)上不可能有两个实数根,应舍去.
当a>0时,令g′(x)=0,解得x=$\frac{1}{4a}$.
令g′(x)>0,解得0<x<$\frac{1}{4a}$,此时函数g(x)单调递增;
令g′(x)<0,解得x>$\frac{1}{4a}$,此时函数g(x)单调递减.
∴当x=$\frac{1}{4a}$时,函数g(x)取得极大值.
当x趋近于0与x趋近于+∞时,g(x)→-∞,
要使g(x)=0在区间(0,+∞)上有两个实数根,
只需g($\frac{1}{4a}$)=ln$\frac{1}{4a}$>0,解得0<a<$\frac{1}{4}$.
∴实数a的取值范围是(0,$\frac{1}{4}$).
故选:C.
点评 本题考查了利用导数研究函数的单调性极值,考查了等价转化方法,考查了推理能力和计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 16:9 | B. | 9:16 | C. | 27:8 | D. | 8:27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
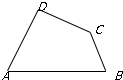 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| B. | 若n组数据(x1,y1)…(xn,yn)的散点都在y=-2x+1上,则相关系数r=-1 | |
| C. | “x0为函数f(x)的极值点”是“f′(x0)=0”的充分不必要条件 | |
| D. | 若随机变量ξ服从二项分布:ξ~B(5,$\frac{1}{5}$),则Eξ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
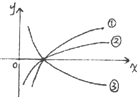 已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )
已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com