
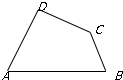
 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.分析 (1)直接利用切化弦以及二倍角公式化简证明即可.
(2)①通过A+C=180°,得C=180°-A,D=180°-B,利用(1)化简tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$=$\frac{2}{sinA}+\frac{2}{sinB}$,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.
②连接AC,利用余弦定理可得1-9cosB=-10cosD,利用三角形面积公式可得S=9sinB+10sinD,平方相加即可解得S2的最大值,进而得解四边形ABCD面积的最大值.
解答 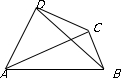 (本题满分为16分)
(本题满分为16分)
解:(1)右=$\frac{1-cosA}{sinA}$=$\frac{1-(1-2si{n}^{2}\frac{A}{2})}{2sin\frac{A}{2}cos\frac{A}{2}}$=$\frac{sin\frac{A}{2}}{cos\frac{A}{2}}$=tan$\frac{A}{2}$=左.…(2分)
(2)①原式$\frac{1-cosA}{sinA}$+$\frac{1-cosB}{sinB}$+$\frac{1-cosC}{sinC}$+$\frac{1-cosD}{sinD}$=$\frac{2}{sinA}+\frac{2}{sinB}$,
连接AC,在△ACD和△ACB中
∴AB2+BC2-2AB•BCcosB=AD2+DC2-2AD•DCcosD,
∴36+9-2×3×3×cosB=25+16+2×5×4×cosB,
∴4=76cosB,∴cosB=$\frac{1}{19}$,∵0<B<π,∴sinB=$\frac{6\sqrt{10}}{19}$.…(4分)
连接BD,在△ABD和△DBC中
∴AD2+AB2-2AD•AB•cosA=CD2+CB2-2CD•CB•cosC,
∴cosA=$\frac{3}{7}$,∵0<A<π,∴sinA=$\frac{2\sqrt{10}}{7}$;…(6分)
∴原式=$\frac{2}{sinA}+\frac{2}{sinB}$=$\frac{4\sqrt{10}}{3}$.…(8分)
②在△ACB和△ACD中,由AB2+BC2-2AB•BCcosB=AC2=AD2+DC2-2AD•DCcosD,
∴36+9-2×6×3×cosB=25+16-2×5×4×cosD,
∴1-9cosB=-10cosD,…(10分)
∵S=$\frac{1}{2}$AB•BC•sinB+$\frac{1}{2}AD•DC•sinD$=$\frac{1}{2}×6×3×sinB+\frac{1}{2}×5×4×sinD$=9sinB+10sinD,…(12分)
∴$\left\{\begin{array}{l}{1-9cosB=-10cosD}\\{S-9sinB=10sinD}\end{array}\right.$,平方相加得1+S2=81+100-180cos(B+D),
所以S2=180-180cos(B+D),当且仅当B+D=π时,S2取最大值360,
所以面积的最大值为6$\sqrt{10}$.…(16分)
点评 本题考查二倍角公式、诱导公式、余弦定理.简单的三角恒等变换,考查函数与方程的思想,转化与化归思想的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a+\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A. | 越大 | B. | 越小 | C. | 无法判定 | D. | 以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
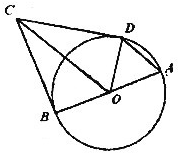 如图,已知AB是圆O的直径,BC与圆O相切与B,D为圆O上的一点,连接DC,DA,CO,DO,∠DAO+∠AOC=180°.
如图,已知AB是圆O的直径,BC与圆O相切与B,D为圆O上的一点,连接DC,DA,CO,DO,∠DAO+∠AOC=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com