
分析 (1)由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解;
(2)由复数的分母不为0,0指数幂的底数不为0联立不等式组求解.
解答 解:(1)由$\left\{\begin{array}{l}{{x}^{2}-2x-15≥0}\\{|x+3|-3≠0}\end{array}\right.$,解得:x≤-3且x≠-6,或x≥5.
∴$f(x)=\frac{{\sqrt{{x^2}-2x-15}}}{{|{x+3}|-3}}$的定义域为(-∞,-6)∪(-6,-3]∪[5,+∞);
(2)由$\left\{\begin{array}{l}{x-1≠0}\\{\frac{1}{x-1}≠-1}\\{2x-1≠0}\end{array}\right.$,解得:x≠0且x$≠\frac{1}{2}$且x≠1.
∴f(x)=$\frac{1}{1+\frac{1}{x-1}}+(2x-1)^{0}$的定义域为(-∞,0)∪(0,$\frac{1}{2}$)∪($\frac{1}{2}$,1).
点评 本题考查函数的定义域及其求法,是基础的计算题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
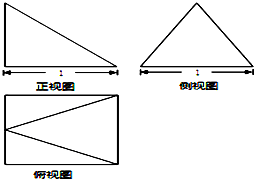
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
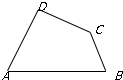 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| B. | 若n组数据(x1,y1)…(xn,yn)的散点都在y=-2x+1上,则相关系数r=-1 | |
| C. | “x0为函数f(x)的极值点”是“f′(x0)=0”的充分不必要条件 | |
| D. | 若随机变量ξ服从二项分布:ξ~B(5,$\frac{1}{5}$),则Eξ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 7 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com