
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据“p且q”与“?p或q”均为假命题,结合复合命题的真值表,易判断命题p与q的真假,根据原命题与其否定之间的关系,即得答案;
②根据二次函数的单调性,利用充分条件和必要条件的定义进行判断即可;
③由零点存在性定理,通过f(-1)•f(1)<0,即可得出结论;
④由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$<0且$\overrightarrow{a}$与$\overrightarrow{b}$不共线,解不等式排除共线的情形即可.
解答 解:对于①,若“p且q”为假命题,则p与q存在假命题,
又“?p或q”为假命题,则?p与q均为假命题,故p真q假,命题①正确;
对于②,如图所示,当a>0时,f(x)=|ax2-x|=|a(x2-x)|=|a(x-$\frac{1}{2a}$)2-$\frac{1}{4a}$|,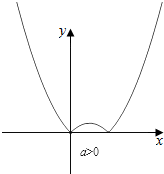
则函数f(x)的对称轴为x=$\frac{1}{2a}$>0,
又f(x)=|ax2-x|=|ax(x-$\frac{1}{a}$)|=0得两个根分别为x=0或x=$\frac{1}{a}$>0,
∴函数f(x)=|ax2-x|在区间(-∞,0)内单调递减,充分性成立;
当a=0时,函数f(x)=|ax2-x|=|x|,满足在区间(-∞,0)上单调递减”,必要性不成立;
∴“a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)内单调递减”的充分不必要条件,命题②错误;
对于③,函数f(x)=3ax+1-2a在(-1,1)上存在x0,使f(x0)=0,
由零点存在性定理,可知f(-1)•f(1)<0,即(-3a+1-2a)•(3a+1-2a)<0;
解得a<-1或a>$\frac{1}{5}$,命题③正确;
④若向量$\overrightarrow a=({-1,2,3}),\overrightarrow b=({2,m,-6})$,且$\overrightarrow a$与$\overrightarrow b$的夹角为钝角,
∴$\overrightarrow{a}$•$\overrightarrow{b}$<0且$\overrightarrow{a}$与$\overrightarrow{b}$不共线,由$\overrightarrow{a}$•$\overrightarrow{b}$<0可得-2+2m-18<0,
解得m<10,
当$\overrightarrow{a}$与$\overrightarrow{b}$共线时,$\frac{-1}{2}$=$\frac{2}{m}$=$\frac{3}{-6}$,可得m=-4,
∴实数m的取值范围为:m<10且m≠-4,命题④错误.
综上,正确的命题序号是①③.
故选:B.
点评 本题考查了复合命题与二次函数的图象与性质的应用问题,也考查了函数零点的定义以及空间向量的应用问题,是综合性题目.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:选择题
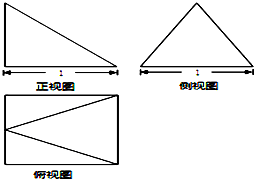
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 8 | C. | 4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
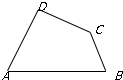 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com