
分析 (1)利用待定系数法,列方程组解出a,b;
(2)先求出l平行x轴和垂直x轴的特殊情况,找到两圆的公共点,再证明此公共点在动圆上即可.
解答 解:(1)设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$,(a>b>0).
∴椭圆的上顶点为B(0,a),右顶点为A(b,0),直线AB的方程为$\frac{x}{b}+\frac{y}{a}$=1.
∴$\left\{\begin{array}{l}{\frac{1}{2}ab=\frac{\sqrt{2}}{2}}\\{\frac{-2}{b}+\frac{3\sqrt{2}}{a}=1}\end{array}\right.$,解得a=$\sqrt{2}$,b=1.
椭圆C的方程是$\frac{{y}^{2}}{2}+{x}^{2}$=1.
(2)若直线与x轴重合,则MN=2b=2,圆的方程为x2+y2=1,
若直线垂直于x轴,则MN=$\frac{8}{3}$,圆的方程为(x+$\frac{1}{3}$)2+y2=$\frac{16}{9}$.
显然A(1,0)为两圆的公共点,
因此所求的点T如果存在,只能是A(1,0).
事实上,点(1,0)就是所求的点.证明如下:
当直线斜率存在时,设直线方程为y=k(x+$\frac{1}{3}$).
由联立方程组$\left\{\begin{array}{l}{\frac{{y}^{2}}{2}+{x}^{2}=1}\\{y=k(x+\frac{1}{3})}\end{array}\right.$,得(k2+2)x2+$\frac{2{k}^{2}}{3}$x+$\frac{{k}^{2}}{9}$-2=0,
设M(x1,y1),N(x2,y2),则x1+x2=-$\frac{2{k}^{2}}{3({k}^{2}+2)}$,x1x2=$\frac{\frac{{k}^{2}}{9}-2}{{k}^{2}+2}$.
又y1y2=k2(x1+$\frac{1}{3}$)(x2+$\frac{1}{3}$)=k2x1x2+$\frac{{k}^{2}}{3}$(x1+x2)+$\frac{{k}^{2}}{9}$.
∵$\overrightarrow{AM}$=(x1-1,y1),$\overrightarrow{AN}$=(x2-1,y2),
∴$\overrightarrow{AM}•\overrightarrow{AN}$=(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+k2x1x2+$\frac{{k}^{2}}{3}$(x1+x2)+$\frac{{k}^{2}}{9}$
=(1+k2)x1x2+($\frac{{k}^{2}}{3}-1$)(x1+x2)+1+$\frac{{k}^{2}}{9}$
═(1+k2)•$\frac{{k}^{2}-18}{9({k}^{2}+2)}$-$\frac{{k}^{2}-3}{3}$•$\frac{2{k}^{2}}{3({k}^{2}+2)}$+$\frac{{k}^{2}+9}{9}$
=0,
∴AM⊥AN,即以MN为直径的圆经过点A(1,0).
所以在坐标平面上存在一个定点T(1,0),使得无论l如何转动,以MN为直径的圆恒过点T.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a+\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
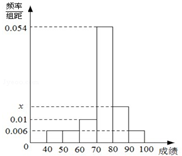 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com