Question

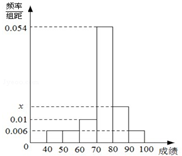
10．某班50位学生期中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中x的值；
（2）根据频率直方分布图计算该班50位学生期中考试数学成绩的平均数；
（3）从成绩低于60分的学生中随机选取2人，求该2人中恰好只有1人成绩在[50，60）的概率．

Answer 1

分析 （1）由频率之和为1，即可求出x的值．
（2）根据平均分的定义即求出，
（3）求出[50，60）上3人，[40，50）上3人，根据条件概率公式计算即可．

解答 解：（1）由30×0.006+10×0.01+10×0.054+10x=1，得x=0.018，
（2）平均分的估计值为0.06×45+0.06×55+0.1×65+0.54×75+0.18×85+0.06×95=74，
（3）0.06×50×2=6，即[50，60）3人，[40，50）3人，
故p=$\frac{{{C}_{3}^{1}C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$．

点评 本题考查了频率分布直方图的应用问题，也考查了平均数中位数的计算问题，考查条件概率问题，是基础题目．