
| A. | $[kπ-\frac{π}{3},kπ+\frac{π}{6}](k∈Z)$ | B. | $[kπ,kπ+\frac{π}{2}](k∈Z)$ | C. | $[kπ+\frac{π}{6},kπ+\frac{2π}{3}](k∈Z)$ | D. | $[kπ-\frac{π}{2},kπ](k∈Z)$ |
分析 由|f($\frac{π}{6}$)|=1及φ的范围求出f(x)的解析式,根据这些函数的单调区间列出不等式组解出.
解答 解:∵f(x)≤|f($\frac{π}{6}$)|对x∈R恒成立,
∴f($\frac{π}{6}$)=1或f($\frac{π}{6}$)=-1.
∴$\frac{π}{3}$+φ=$\frac{π}{2}$+kπ,即φ=$\frac{π}{6}$+kπ,k∈Z.
∵$\frac{π}{2}$<|φ|<π,
∴φ=-$\frac{5π}{6}$.
∴f(x)=sin(2x-$\frac{5π}{6}$),
令-$\frac{π}{2}$+2kπ≤2x-$\frac{5π}{6}$≤$\frac{π}{2}$+2kπ,解得$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ,
故选C.
点评 本题考查了三角函数的性质,求出φ的值是解题关键,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A. | 越大 | B. | 越小 | C. | 无法判定 | D. | 以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 18 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
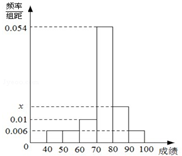 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com