Question

3．平行四边形ABCD中，对角线AC=$\sqrt{65}，BD=\sqrt{17}$，周长为18，则这个平行四边形的面积是（　　）

• A． 8
• B． 18
• C． 16
• D． 32

Answer 1

分析 可设AB=a，BC=b，从而得出a+b=9，进而得到a²+b²+2ab=81①，分别在△ABC和△BCD中，由余弦定理得到AC²=a²+b²-2abcos∠ABC，BD²=a²+b²-2abcos∠BCD，从而得出a²+b²=41②，联立①便可得到ab=20，而联立a+b=9即可求出a，b，进而根据余弦定理求出cos∠ABC，然后得出sin∠ABC，从而求出平行四边形的面积．

解答 解：如图，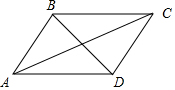

设AB=CD=a，AD=BC=b，由周长为18，得到a+b=9；
∴（a+b）²=a²+b²+2ab=81①；
∵∠ABC+∠BCD=180°；
∴由余弦定理得：AC²+BD²=a²+b²-2abcos∠ABC+a²+b²-2abcos∠BCD=2（a²+b²）=65+17=82；
即a²+b²=41②；
②代入①得：ab=20，与a+b=9联立，解得：a=4，b=5；
在△ABC中，AB=4，BC=5，$AC=\sqrt{65}$；
∴由余弦定理得，$cos∠ABC=\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}=\frac{16+25-65}{2×4×5}$=$-\frac{3}{5}$；
∴$sin∠ABC=\frac{4}{5}$；
∴${S}_{平行四边形ABCD}=AB•BCsin∠ABC4×5×\frac{4}{5}=16$．
故选：C．

点评 考查平行四边形边的关系，余弦定理，三角函数诱导公式，以及三角形的面积公式．