练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知全集U={1，2，3，6}，集合A={1，3}，则∁UA={2，6}．

    分析 根据补集的定义求得∁UA．

    解答 解：全集U={1，2，3，6}，集合A={1，3}，则∁UA={2，6}．
    故答案为：{2，6}．

    点评 本题主要考查补集的定义和求法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知光线经过已知直线l1：3x-y+7=0和l2：2x+y+3=0的交点M，且射到x轴上一点N（1，0）后被x轴反射．
    （1）求点M关于x轴的对称点P的坐标；
    （2）求反射光线所在的直线l3的方程．
    （3）求与l3距离为$\sqrt{10}$的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．对于实数x∈（0，$\frac{π}{2}$），f（x）=$\frac{1}{{9{{sin}^2}x}}$+$\frac{4}{{9{{cos}^2}x}}$．
    （1）若f（x）≥t恒成立，求t的最大值M；
    （2）在（1）的条件下，求不等式x2+|x-2|+M≥3的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．一个圆锥与一个球的体积相等，圆锥的底面半径是球半径的$\frac{3}{2}$倍，则圆锥的高与球半径之比为（　　）
    A．16：9B．9：16C．27：8D．8：27

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．抛物线y2=$\frac{1}{4}$x上一点M到焦点的距离为1，则点M的横坐标为$\frac{15}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．一个棱锥的三视图如图所示，其中侧视图为正三角形，则该四棱锥的体积是（　　）
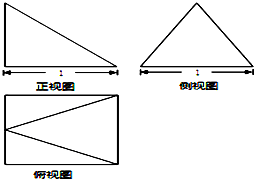
    A．$\frac{1}{3}$B．$\frac{{\sqrt{3}}}{2}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{{\sqrt{3}}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．为评估设备M生产某种零件的性能，从设备M生产零件的流水线上随机抽取100件零件作为样本，测量其直径后，整理得到下表：
    直径/mm5859616263646566676868707173合计
    件数11356193318442121100
    经计算，样本的平均值μ=65，标准差σ=2.2，以频率值作为概率的估计值．
    （Ⅰ）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为X，并根据以下不等式进行评判（P表示相应事件的概率）：①P（μ-σ＜X≤μ+σ）≥0.6826；②P（μ-2σ＜X≤μ+2σ）≥0.9544；③P（μ-3σ＜X≤μ+3σ）≥0.9974．评判规则为：若同时满足上述三个不等式，则设备等级为甲；若仅满足其中两个，则等级为乙；若仅满足其中一个，则等级为丙；若全部都不满足，则等级为丁．试判断设备M的性能等级．
    （Ⅱ）将直径小于等于μ-2σ或直径大于μ+2σ的零件认为是次品．
    （i）从设备M的生产流水线上随意抽取2件零件，计算其中次品个数Y的数学期望EY；
    （ii）从样本中随意抽取2件零件，计算其中次品个数Z的数学期望EZ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}的前n项和为Sn，且a1=1，an=$\frac{2S_n^2}{{2{S_n}-1}}（{n≥2}）$．
    （Ⅰ）求证：$\left\{{\frac{1}{S_n}}\right\}$是等差数列，并求Sn的表达式；
    （Ⅱ）若存在正数k，使得对任意n∈N*，都有（1+S1）（1+S2）…（1+Sn）≥k$\sqrt{2n+1}$，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列判断错误的是（　　）
    A．若随机变量ξ服从正态分布N（1，σ2），P（ξ≤4）=0.79，则P（ξ≤-2）=0.21
    B．若n组数据（x1，y1）…（xn，yn）的散点都在y=-2x+1上，则相关系数r=-1
    C．“x0为函数f（x）的极值点”是“f′（x0）=0”的充分不必要条件
    D．若随机变量ξ服从二项分布：ξ～B（5，$\frac{1}{5}$），则Eξ=1

    查看答案和解析>>

    同步练习册答案