
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 68 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
分析 (Ⅰ)利用条件,可得设备M的数据仅满足一个不等式,即可得出结论;
(Ⅱ)易知样本中次品共6件,可估计设备M生产零件的次品率为0.06.
(ⅰ)由题意可知Y~B(2,$\frac{6}{100}$)),可得EY=2×$\frac{6}{100}$.
(ⅱ)确定Z的取值,利用超几何分布可得相应的概率,即可求出其中次品个数Z的数学期望EZ.
解答 解:(Ⅰ)P(μ-σ<X≤μ+σ)=P(62.8<X≤67.2)=0.8>0.6826,
P(μ-2σ<X≤μ+2σ)=P(60.6<X≤69.4)=0.94<0.9544,
P(μ-3σ<X≤μ+3σ)=P(58.4<X≤71.6)=0.98<0.9974,
∵设备M的数据仅满足一个不等式,故其性能等级为丙.
样本中次品共6件,可估计设备M生产零件的次品率为0.06.
(ⅰ)由题意可知Y~B(2,$\frac{6}{100}$)),于是EY=2×$\frac{6}{100}$=$\frac{3}{25}$.
(ⅱ)由题意可知Z的分布列为
| Z | 0 | 1 | 2 |
| P | $\frac{{∁}_{94}^{2}}{{∁}_{100}^{2}}$ | $\frac{{∁}_{6}^{1}{∁}_{94}^{1}}{{∁}_{100}^{2}}$ | $\frac{{∁}_{6}^{2}}{{∁}_{100}^{2}}$ |
点评 本题考查了二项分布列及其数学期望、正态分布曲线的性质,考查推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
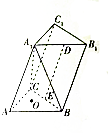 如图所示,在三棱柱ABC-A1B1C1中,底面△ABC是边长为6的等边三角形,点A1
如图所示,在三棱柱ABC-A1B1C1中,底面△ABC是边长为6的等边三角形,点A1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com