
分析 由题意y=f(x)是定义在R上的偶函数,满足f(x+1)=-f(x),可以知道该函数的周期为2,在利用f(x)为偶函数且在[-1,0]上为增函数,可以由题意画出一个草图即可判断.
解答 解:因为f(x+1)=-f(x) 所以f(x+2)=-f(x+1)=f(x),
由函数的周期定义可知该函数的周期为2,
由于f(x)为定义在R上的偶函数且在[-1,0]上为单调递增函数,
所以由题意可以画出一下的函数草图为: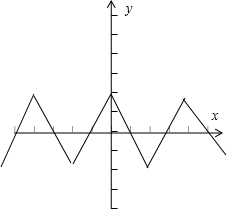
由图及题中条件可以得到:
①正确,周期T=2;
②由图可以知道该函数关于x=1对称,所以②正确;
③有已知条件 y=f(x)是定义在R上的偶函数且在[-1,0]上是增函数,
所以y=f(x)在[0,1]上为单调递减函数,故③错,
故答案为:①②.
点评 此题考查了函数的周期性,对称性及有抽象函数式子赋值的方法,还考查了学生对于抽象问题的具体化及数形结合的思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
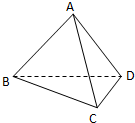 如图,直二面角A-BD-C,平面ABD⊥平面BCD,若其中给定 AB=AD=2,∠BAD=90°,∠BDC=60°,BC⊥CD.
如图,直二面角A-BD-C,平面ABD⊥平面BCD,若其中给定 AB=AD=2,∠BAD=90°,∠BDC=60°,BC⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
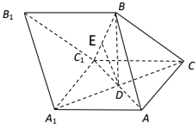 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 68 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com