
分析 (1)求出导数,设出切点(m,n),求得切线的斜率,由切线的方程,可得a=em(2m+1),又n=am-a=em(2m-1),解方程可得a的值;
(2)f(x)≥g(x)可化为ex(2x-1)≥a(x-1),当x-1=0,即x=1时,e>0恒成立,a∈R;当x-1>0,即x>1时,$a≤\frac{{{e^x}(2x-1)}}{x-1}$恒成立,构造函数求最值,即可得出a的取值范围.
解答 解:(1)f′(x)=ex(2x-1)+2ex=ex(2x+1),
设切点为(m,n),由题意可得a=em(2m+1),
又n=am-a=em(2m-1),
解方程可得,a=1或$4{e}^{\frac{3}{2}}$.
(2)f(x)≥g(x)可化为ex(2x-1)≥a(x-1),
当x-1=0,即x=1时,e>0恒成立,a∈R;
当x-1>0,即x>1时,$a≤\frac{{{e^x}(2x-1)}}{x-1}$恒成立,
令$F(x)=\frac{{{e^x}(2x-1)}}{x-1}$,则$F'(x)=\frac{{{e^x}(2{x^2}-3x)}}{{{{(x-1)}^2}}}$,∴$F(x)在({1,\;\;\frac{3}{2}})上递减,在({\frac{3}{2},\;\;+∞})上递增$,∴$F{(x)_{min}}=F({\frac{3}{2}})=4{e^{\frac{3}{2}}}$,∴$a≤4{e^{\frac{3}{2}}}$;
当x-1<0,即x<1时,$a≥\frac{{{e^x}(2x-1)}}{x-1}$恒成立,
令$F(x)=\frac{{{e^x}(2x-1)}}{x-1}$,则$F'(x)=\frac{{{e^x}(2{x^2}-3x)}}{{{{(x-1)}^2}}}$,∴F(x)在(-∞,0)上递增,在(0,1)上递减,∴F(x)max=F(0)=1,∴a≥1,
综上所述:$1≤a≤4{e^{\frac{3}{2}}}$.
点评 本题考查导数的运用:求切线的斜率和极值、最值,涉及数形结合和转化的思想,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
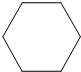 已知正六棱柱的底面边长和侧棱长相等,体积为96$\sqrt{3}$,其三视图中的俯视图如图所示,则其左视图的面积是( )
已知正六棱柱的底面边长和侧棱长相等,体积为96$\sqrt{3}$,其三视图中的俯视图如图所示,则其左视图的面积是( )| A. | $8\sqrt{3}$ | B. | 16 | C. | $16\sqrt{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 68 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | -48 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com