
分析 (1)把点的坐标代入f(x)计算;
(2)对f(x)的对称轴与区间[-1,2]的关系进行分情况讨论,判断f(x)的单调性,利用单调性解出b,再求出最大值.
解答 解:(1)把(4,3)代入f(x)得16-8b+3=3,∴b=2.
(2)f(x)的图象开口向上,对称轴为x=b.
①若b≤-1,则f(x)在[-1,2]上是增函数,
∴fmin(x)=f(-1)=4+2b=1,解得b=-$\frac{3}{2}$.
∴fmax(x)=f(2)=7-4b=13.
②若b≥2,则f(x)在[-1,2]上是减函数,
∴fmin(x)=f(2)=7-4b=1,解得b=$\frac{3}{2}$(舍).
③若-1<b<2,则f(x)在[-1,b]上是减函数,在(b,2]上增函数.
∴fmin(x)=f(b)=-b2+3=1,解得b=$\sqrt{2}$或b=-$\sqrt{2}$(舍).
∴fmax(x)=f(-1)=4+2b=4+2$\sqrt{2}$.
综上,当b≤-1时,f(x)的最大值为13,当-1<b<2时,f(x)最大值为4+2$\sqrt{2}$.
点评 本题考查了二次函数的单调性与对称轴的关系,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ¬q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{4}{9}$,1] | B. | [$\frac{4}{9}$,1] | C. | ($\frac{4}{9}$,+∞) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
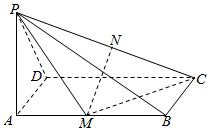 如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.
如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com