
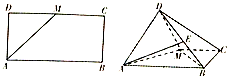
分析 (1)取AD的中点F,连接EF,MF,CE,证明四边形EFMC是平行四边形得出CE∥MF,故而CE∥平面AMD;
(2)E为DB的中点,故VM-ADE=VE-ADM=$\frac{1}{2}$VB-ADM,证明BM⊥平面ADM,于是VM-ADE=$\frac{1}{6}$S△ADM•BM.
解答 证明:(1)取AD的中点F,连接EF,MF,CE,则EF∥AB且EF=$\frac{1}{2}$AB.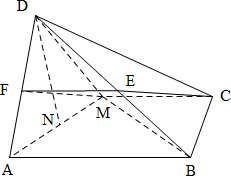
又MC∥AB且MC=$\frac{1}{2}$AB,
∴EF∥MC,EF=MC,
∴四边形EFMC是平行四边形,
∴CE∥MF,
又CE?平面ADM,MF?平面ADM,
∴CE∥平面ADM.
(2)∵AD=DM=CM=BC=1,∠ADM=∠BCM=90°,
∴AM=BM=$\sqrt{2}$,又AB=2,
∴AM2+BM2=AB2,即AM⊥BM,
又平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM,
∴VB-ADM=$\frac{1}{3}$S△ADM•BM=$\frac{1}{3}×\frac{1}{2}×{1}^{2}×\sqrt{2}$=$\frac{\sqrt{2}}{6}$.
∵$\overrightarrow{DE}$=$\overrightarrow{EB}$,∴E为DB的中点,
∴VM-ADE=VE-ADM=$\frac{1}{2}$VB-ADM=$\frac{\sqrt{2}}{12}$.
点评 本题考查了线面平行的判定,线面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
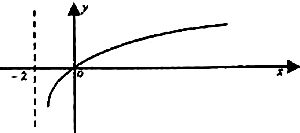 函数f(x)的定义域为(-2,+∞),部分对应值如表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,若正数a,b满足f(2a+b)<1,则$\frac{b+2}{a+2}$的取值范围是($\frac{1}{2}$,3)
函数f(x)的定义域为(-2,+∞),部分对应值如表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,若正数a,b满足f(2a+b)<1,则$\frac{b+2}{a+2}$的取值范围是($\frac{1}{2}$,3)| x | -1 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com