
���� ��1������������������ak��ak+1��ak+2�ɵȲ����У�k��N*����2ak+1=ak+ak+2�����뻯�ɵó���
��2����a1��ar��as�ɵȲ����У���2[2r-��-1��r]=3+2s-��-1��s�����ɵó���
��3������an+1-an=2n+1-��-1��n+1-2n+��-1��n=2n+2��-1��n��0��������aq��ar��as��at�ɵȲ����У�����1��q��r��s��t������aq+at=ar+as����2q-��-1��q+2t-��-1��t=2r-��-1��r+2s-��-1��s�����ɵó���
��� �⣺��1������������������ak��ak+1��ak+2�ɵȲ����У�k��N*��
��2ak+1=ak+ak+2��
����2[2k+1-��-1��k+1]=2k-��-1��k+2k+2-��-1��k+2������1�֣�
����2k=-4��-1��k������2�֣�
����=-4��-1��k=��4����2k=4����k=2��
���Ե��ҽ���k=2ʱ��ak��ak+1��ak+2�ɵȲ����С���4�֣�
��2����a1��ar��as�ɵȲ����У���2[2r-��-1��r]=3+2s-��-1��s��
��2s-2r+1=��-1��s-2��-1��r-3����6�֣�
��r��s����2s-2r+1��0��
����-1��s-2��-1��r-3��0������8�֣�
��2s-2r+1=0���ɵ�s=r+1����sΪ���ڵ���4��ż������10�֣�
��3������an+1-an=2n+1-��-1��n+1-2n+��-1��n=2n+2��-1��n��0������12�֣�
������aq��ar��as��at�ɵȲ����У�����1��q��r��s��t��
����aq+at=ar+as����2q-��-1��q+2t-��-1��t=2r-��-1��r+2s-��-1��s��
����2q+2t-2r-2s=��-1��q+��-1��t-��-1��r-��-1��t����*��
��Ϊ��*��ʽ��ߡ�22+2=6��
��*��ʽ�ұߡ�4��
���ԣ�*��ʽ�⣬��������{an}�в�����ij4��ɵȲ����С���16�֣�
���� ���⿼���˵Ȳ�������ȱ����е�ͨ�ʽ������ʽ�Ľⷨ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��3] | B�� | ��0��3�� | C�� | [0��3] | D�� | [3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ln2 | B�� | ln2+1 | C�� | 1 | D�� | $\frac{{{e^2}-1}}{{4{e^2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ֱ�ߺ�ͬһ��ƽ��ƽ�У���������ֱ��ƽ�� | |
| B�� | ��һֱ��������ƽ�����ɵĽ���ȣ���������ƽ��ƽ�� | |
| C�� | ��һ��ֱ��ƽ���������ཻƽ�棬������ֱ����������ƽ��Ľ���ƽ�� | |
| D�� | ������ƽ�洹ֱ��ͬһ��ƽ�棬��������ƽ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
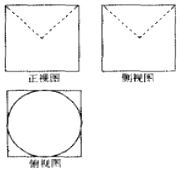 ij�����������ͼ��ͼ��ʾ��ͼ���ı��ζ��DZ߳�Ϊ2�������Σ������������ֱ����ü�����ı�����ǣ�������
ij�����������ͼ��ͼ��ʾ��ͼ���ı��ζ��DZ߳�Ϊ2�������Σ������������ֱ����ü�����ı�����ǣ�������| A�� | $24+��{\sqrt{2}+1}����$ | B�� | $24+��{\sqrt{2}-1}����$ | C�� | $24-��{\sqrt{2}+1}����$ | D�� | $24-��{\sqrt{2}-1}����$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com