
【题目】已知两定点![]() ,满足条件
,满足条件![]() 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点,
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点,
(1)求k的取值范围;
(2)如果![]() ,且曲线E上存在点C,使
,且曲线E上存在点C,使![]() ,求m的值和
,求m的值和![]() 的面积S。
的面积S。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,面积为
,面积为![]() .
.
【解析】
试题(1)由双曲线的定义可知,曲线![]() 是以
是以![]() 为焦点的双曲线的左支,
为焦点的双曲线的左支,![]() ,所以方程为
,所以方程为![]() ;(2)由于直线和双曲线相交于左支,且有两个交点,故联立直线的方程和双曲线的方程,消去
;(2)由于直线和双曲线相交于左支,且有两个交点,故联立直线的方程和双曲线的方程,消去![]() 后得到关于
后得到关于![]() 的一元二次方程的判别式大于零,且韦达定理两根的和小于零,两根的积大于零,由此列不等式组,求解的
的一元二次方程的判别式大于零,且韦达定理两根的和小于零,两根的积大于零,由此列不等式组,求解的![]() 的取值范围;(3)利用弦长公式计算得直线斜率为
的取值范围;(3)利用弦长公式计算得直线斜率为![]() .由题设向量关系,得到
.由题设向量关系,得到![]() ,代入双曲线方程,求得
,代入双曲线方程,求得![]() ,利用面积公式求得面积为
,利用面积公式求得面积为![]() .
.
试题解析:
(1)由双曲线的定义可知,曲线![]() 是以
是以![]() 为焦点的双曲线的左支,且
为焦点的双曲线的左支,且![]() ,易知
,易知![]()
故曲线![]() 的方程为
的方程为![]()
(2)设![]() ,由题意建立方程组
,由题意建立方程组![]()
消去![]() ,得
,得![]()
又已知直线与双曲线左支交于两点![]() ,有
,有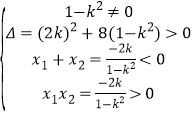 解得
解得![]()
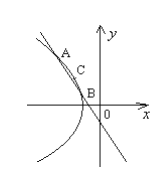
(3)
![]()
依题意得![]()
整理后得![]()
∴![]() 或
或![]()
但![]() ∴
∴![]()
故直线![]() 的方程为
的方程为![]()
设![]() ,由已知
,由已知![]() ,得
,得![]()
∴![]()
又![]()
∴点![]()
将点![]() 的坐标代入曲线
的坐标代入曲线![]() 的方程,得
的方程,得![]() 得
得![]() ,
,
但当![]() 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴![]() ,点的坐标为
,点的坐标为![]()
![]() 到
到![]() 的距离为
的距离为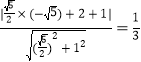
∴![]() 的面积
的面积![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某一段海底光缆出现故障,需派人潜到海底进行维修,现在一共有甲、乙、丙三个人可以潜水维修,由于潜水时间有限,每次只能派出一个人,且每个人只派一次,如果前一个人在一定时间内能修好则维修结束,不能修好则换下一个人.已知甲、乙、丙在一定时间内能修好光缆的概率分别为![]() ,且各人能否修好相互独立.
,且各人能否修好相互独立.
(1)若按照丙、乙、甲的顺序派出维修,设所需派出人员的数目为X,求X的分布列和数学期望;
(2)假设三人被派出的不同顺序是等可能出现的,现已知丙在乙的下一个被派出,求光缆被丙修好的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动点
,动点![]() 在圆
在圆![]() 上运动,点
上运动,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求点![]() 的轨迹方程.
的轨迹方程.
(2)过点![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,
, ![]() ,分别与圆
,分别与圆![]() 相切于点
相切于点![]() ,
, ![]() ,求直线
,求直线![]() 的方程,并判断直线
的方程,并判断直线![]() 与点
与点![]() 所在曲线的位置关系.
所在曲线的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)若回归直线方程![]() ,其中
,其中![]() ;试预测当单价为10元时的销量;
;试预测当单价为10元时的销量;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果3位女生都相邻,且男生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只苍蝇和![]() 只蜘蛛被放置在
只蜘蛛被放置在![]() 方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
(1)找出最小的正整数![]() ,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
(2)在![]() 的空间三维方格中,(1)中的结论又是怎样?
的空间三维方格中,(1)中的结论又是怎样?
(注)题中相邻是指一个交点仅有一个坐标与另一个交点的同一坐标不同,且差值为1;题中抓住是指蜘蛛和苍蝇位于同一交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com