
【题目】一只苍蝇和![]() 只蜘蛛被放置在
只蜘蛛被放置在![]() 方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
(1)找出最小的正整数![]() ,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
(2)在![]() 的空间三维方格中,(1)中的结论又是怎样?
的空间三维方格中,(1)中的结论又是怎样?
(注)题中相邻是指一个交点仅有一个坐标与另一个交点的同一坐标不同,且差值为1;题中抓住是指蜘蛛和苍蝇位于同一交点.
【答案】(1)2 (2)见解析
【解析】
(1)首先证明,一只蜘蛛无法捉到苍蝇.
建立直角坐标系,则蜘蛛、苍蝇活动的范围是![]() .
.
对于上述集合中的每个点,至少存在两个集合中的点和它相邻.因此,若某次蜘蛛行动之后与苍蝇不相邻,则苍蝇不动即可;若某次蜘蛛行动后与苍蝇相邻,则它只需进入与其所在点相邻的另一个上述集合中的点.这样蜘蛛捉不到苍蝇.
其次,若有两只蜘蛛![]() 、
、![]() ,记
,记![]() 与苍蝇
与苍蝇![]() 在
在![]() 次移动后的距离为
次移动后的距离为![]() ,其中,定义两点
,其中,定义两点![]() 与
与![]() 的距离为
的距离为![]() .
.
首先,可以通过若干次操作使得![]() .
.
接下来证明:
(ⅰ)每次移动后,可适当移动![]() 、
、![]() ,使得
,使得![]() 处于以
处于以![]() 、
、![]() 为对角线的矩形内部或边界上(
为对角线的矩形内部或边界上(![]() 、
、![]() 的连线不平行于坐标轴);
的连线不平行于坐标轴);
(ⅱ)保持![]() 不增,且若干次后必严格减少.
不增,且若干次后必严格减少.
事实上,记![]() 、
、![]() 轴正方向的单位向量为
轴正方向的单位向量为![]() 、
、![]() .则策略如下:
.则策略如下:
若某次苍蝇移动后某坐标值不在以![]() 、
、![]() 为对角线的矩形内部或者边界上,则
为对角线的矩形内部或者边界上,则![]() 、
、![]() 同时沿该方向朝
同时沿该方向朝![]() 所在的方格移动;否则,
所在的方格移动;否则,![]() 只要移动
只要移动![]() 或
或![]() ,
,![]() 只要移动
只要移动![]() 或
或![]() ,适当选择使
,适当选择使![]() 、
、![]() 的连线不平行于坐标轴,且保持苍蝇的位置位于上述矩形的内部或边界上.由归纳法易证(ⅰ).
的连线不平行于坐标轴,且保持苍蝇的位置位于上述矩形的内部或边界上.由归纳法易证(ⅰ).
下面证明(ⅱ).
事实上,若![]() 在
在![]() 次操作前严格位于以
次操作前严格位于以![]() 、
、![]() 为对角线的矩形内,则该轮次后,
为对角线的矩形内,则该轮次后,![]() 必减;否则,
必减;否则,![]() 必在矩形的某边上且它必须向矩形外移动,由规则知此时
必在矩形的某边上且它必须向矩形外移动,由规则知此时![]() 不增,但方格表有界,因此,至多在4024步以后
不增,但方格表有界,因此,至多在4024步以后![]() 不能再向矩形外移动.此时,
不能再向矩形外移动.此时,![]() 严格减少.
严格减少.
因为![]() 的初始值为4024,不能无限下降,所以,经过有限步操作后蜘蛛能够抓到苍蝇.
的初始值为4024,不能无限下降,所以,经过有限步操作后蜘蛛能够抓到苍蝇.
(2)结论不变,![]() 的最小值仍为2.
的最小值仍为2.
建立空间直角坐标系,则![]() 、
、![]() 的范围是
的范围是![]() .
.
当![]() 时,令
时,令![]() 、
、![]() 通过若干次操作分别到
通过若干次操作分别到![]() 与
与![]() ,且每次操作保持
,且每次操作保持![]() 在以
在以![]() 、
、![]() 为体对角线的立方体内部或边界(面、棱、顶点)上,且
为体对角线的立方体内部或边界(面、棱、顶点)上,且![]() 、
、![]() 的连线不平行于平面
的连线不平行于平面![]() 、
、![]() 、
、![]() .完全类似可证:每次操作后
.完全类似可证:每次操作后![]() 不增,且至多经过
不增,且至多经过![]() 步后,必定严格减少.
步后,必定严格减少.
而初始的![]() ,故经过有限步也必定结束操作,蜘蛛抓住苍蝇.
,故经过有限步也必定结束操作,蜘蛛抓住苍蝇.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为![]() ,参加第五项不合格的概率为
,参加第五项不合格的概率为![]()
(1)求该生被录取的概率;
(2)记该生参加考试的项数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,满足条件
,满足条件![]() 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点,
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A,B两点,
(1)求k的取值范围;
(2)如果![]() ,且曲线E上存在点C,使
,且曲线E上存在点C,使![]() ,求m的值和
,求m的值和![]() 的面积S。
的面积S。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
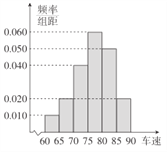
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .将曲线
.将曲线![]() 上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线
上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考虑![]() 的方格表,其中每个方格内均填有数字0.每次操作可先选定三个实数
的方格表,其中每个方格内均填有数字0.每次操作可先选定三个实数![]() 、
、![]() 、
、![]() ,然后选定一行,将这一行每个方格中的数都加上
,然后选定一行,将这一行每个方格中的数都加上![]() (
(![]() 为该方格所在的列数,
为该方格所在的列数,![]() );或选定一列,将这一列每个方格中的数都加上
);或选定一列,将这一列每个方格中的数都加上![]() (
(![]() 为该方格所在的行数,
为该方格所在的行数,![]() ),问:能否经过有限次操作,使该方格表中四个角的数字变成1,而其他格的数字仍为0?
),问:能否经过有限次操作,使该方格表中四个角的数字变成1,而其他格的数字仍为0?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次会操活动中,领操员让编号为![]() 的
的![]() 名学生排成一个圆形阵,做
名学生排成一个圆形阵,做![]() 循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为
循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为![]() 的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
(1)最后留在场内的学生最初的编号是几号?
(2)求领操员记录下的编号之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com