
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{2π}{3}$ |
分析 由已知利用两角和的正弦函数公式化简函数解析式可得f(x)=2$\sqrt{3}$sin(4x+$\frac{π}{6}$),利用函数y=Asin(ωx+φ)的图象变换可求g(x)=2$\sqrt{3}$sin(2x-$\frac{π}{6}$),进而利用正弦函数的图象和性质即可得解.
解答 解:∵f(x)=3sin4x+$\sqrt{3}$cos4x=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$sin4x+$\frac{1}{2}$cos4x)=2$\sqrt{3}$sin(4x+$\frac{π}{6}$),
∴将函数f(x)图象上所有点的横坐标变为原来的2倍,得到函数图象对应的解析式为:y=2$\sqrt{3}$sin(2x+$\frac{π}{6}$),
再向右平移$\frac{π}{6}$个单位长度,得到函数图象对应的解析式为:g(x)=2$\sqrt{3}$sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=2$\sqrt{3}$sin(2x-$\frac{π}{6}$),
∴由2x-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得:x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,
∴当k=0时,y=g(x)的图象的对称轴方程是x=$\frac{π}{3}$.
故选:C.
点评 本题主要考查了两角和的正弦函数公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
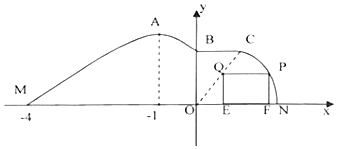 “中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.
“中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
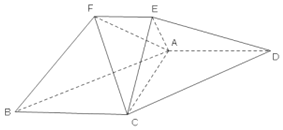 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15m | B. | 30m | C. | 25m | D. | 50m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com