
(本小题满分12分)
已知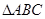 的面积
的面积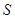 满足
满足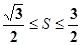 ,且
,且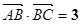 ,
,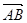 与
与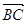 的夹角为
的夹角为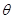 .
.
(1)求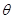 的取值范围;
的取值范围;
(2)求函数 的最大值及最小值.
的最大值及最小值.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分10分)
在△ABC中,角A、B、C所对的边分别为a、b、c,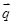 =(
=(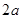 ,1),
,1),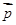 =(
=(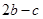 ,
, 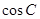 )且
)且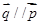 .
.
求:(I)求sin A的值;(II)求三角函数式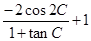 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com