
分析 (1)直线l将圆O分成的两端弧之比为1:3,可得劣弧所对的圆心角为90°,即可求m的值;
(2)由“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”,即可求m的值;
(3)以M为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,即可求出半径最小的圆的方程.
解答 解:(1)∵直线l将圆O分成的两端弧之比为1:3,
∴劣弧所对的圆心角为90°,
∴圆心到直线的距离d=$\frac{|m|}{\sqrt{5}}$=2×$\frac{\sqrt{2}}{2}$,
∴m=±$\sqrt{10}$;
(2)根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,
切线长PA,PB最小.切线长为$\sqrt{5}$,圆心到直线l的距离为3,∴d=$\frac{|m|}{\sqrt{5}}$=3,
∴m=±3$\sqrt{5}$;
(3)以M为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,圆心M为过原点且与l垂直的直线l′与l的交点P0,所以r=3$\sqrt{5}$-2,
又l′:x-2y=0,联立l:2x+y+m=0得P0(-$\frac{6\sqrt{5}}{5}$,-$\frac{3\sqrt{5}}{5}$)或P0(-$\frac{6\sqrt{5}}{5}$,-$\frac{3\sqrt{5}}{5}$).
所以所求圆的方程为(x-$\frac{6\sqrt{5}}{5}$)2+(y-$\frac{3\sqrt{5}}{5}$)2=(3$\sqrt{5}$-2)2或(x+$\frac{6\sqrt{5}}{5}$)2+(y+$\frac{3\sqrt{5}}{5}$)2=(3$\sqrt{5}$-2)2.
点评 本题考查直线与圆的位置关系,考查圆的方程,考查学生分析解决问题的能力,属于中档题.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
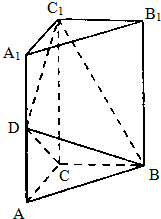 如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}$AA1,D是棱AA1的中点,DC1⊥BD.
如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}$AA1,D是棱AA1的中点,DC1⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{3π}{4}$) | B. | (2$\sqrt{3}$,$\frac{3π}{4}$) | C. | (2$\sqrt{3}$,π) | D. | (3,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又BA1⊥AC1,CC1的中点为E.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又BA1⊥AC1,CC1的中点为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com