
分析 设|BF1|=n,由题意可得|AB|=n,|AF1|=$\sqrt{2}$n,运用双曲线的定义和勾股定理,化简整理,由离心率公式计算即可得到所求值.
解答 解:设|BF1|=n,由|AB|=|BF1|,且∠ABF1=90°,可得
|AB|=n,|AF1|=$\sqrt{2}$n,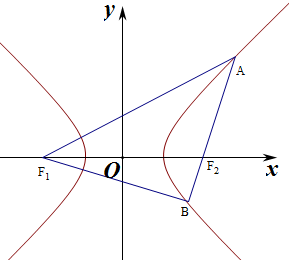
由双曲线的定义可得|BF1|-|BF2|=2a,
即有|BF2|=n-2a,
又|AF1|-|AF2|=2a,可得|AF2|=$\sqrt{2}$n-2a,
由|AB|=($\sqrt{2}$+1)n-4a=n,
解得n=2$\sqrt{2}$a,
在△F1F2B中,由|BF1|2+|BF2|2=|F1F2|2,
即为(2$\sqrt{2}$a)2+(2$\sqrt{2}$-2)2a2=4c2,
化为c2=(5-2$\sqrt{2}$)a2,
可得e=$\frac{c}{a}$=$\sqrt{5-2\sqrt{2}}$,
故答案为:$\sqrt{5-2\sqrt{2}}$,
点评 本题考查双曲线的离心率的求法,运用双曲线的定义和勾股定理是解决本题的关键,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}})$ | B. | (-∞,-1) | C. | $({-\frac{1}{2},+∞})$ | D. | (-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{6}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | ($\frac{π}{6}$,$\frac{2π}{3}$) | D. | ($\frac{π}{3}$,$\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大于m | B. | 小于m | ||
| C. | 等于m | D. | 与m的大小关系无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投入促销费用x(万元) | 2 | 3 | 5 | 6 |
| 商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com