
| A. | 大于m | B. | 小于m | ||
| C. | 等于m | D. | 与m的大小关系无法确定 |
分析 令f(x)=$\sqrt{x}$,根据定义计算近似值比较大小即可.
解答 解:根据题意,令f(x)=$\sqrt{x}$,则f′(x)=$\frac{1}{2\sqrt{x}}$>0,
取4.001附近的点x0=4,则有m的近似代替值为f(4)+$\frac{1}{2\sqrt{4}}$(4.001-4)=2+$\frac{0.001}{4}$,
∵(2+$\frac{0.001}{4}$)2=4+0.001+($\frac{0.001}{4}$)2>4.001=m2,
∴2+$\frac{0.001}{4}$>m.
故选A.
点评 本题考查导数的计算,关键是分析题意,理解“近似代替值”的意义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | A∩B=A | B. | (∁RA)∩B=A | C. | A∩(∁RB)=A | D. | (∁RA)∩(∁RB)=A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
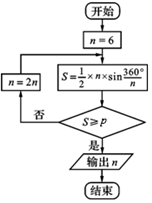 三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )
三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )| A. | 2.6 | B. | 3 | C. | 3.1 | D. | 3.14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=P | B. | P?M | C. | M?P | D. | (∁UM)∩P=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com