
 如图,已知三棱锥D-ABC的底面是正三角形,且DA⊥平面ABC,O为底面中心,M、N是BD上的两点,且BM=DM=3MN
如图,已知三棱锥D-ABC的底面是正三角形,且DA⊥平面ABC,O为底面中心,M、N是BD上的两点,且BM=DM=3MN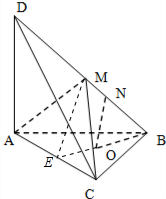 证明:(1)延长BO交AC于E,连接ME,
证明:(1)延长BO交AC于E,连接ME,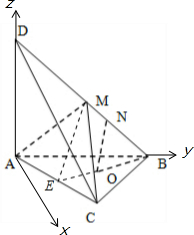
| 3 |
| ||
| 3 |
| BO |
| ||
| 3 |
| AM |
| AC |
| 3 |
| m |
|
|
|
| m |
| 3 |
| 3 |
|
| ||||
|
|
| ||||||
|
2
| ||
| 7 |


科目:高中数学 来源: 题型:
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某县工业园区人才市场举办农民工招聘洽谈活动,某服装厂经过综合测试,录用了14名男工和6名女工,这20名工人的测试成绩如茎叶图所示,服装厂规定:成绩在180分以上者到“甲车间”工作;180分以下者到“乙车间”工作.
某县工业园区人才市场举办农民工招聘洽谈活动,某服装厂经过综合测试,录用了14名男工和6名女工,这20名工人的测试成绩如茎叶图所示,服装厂规定:成绩在180分以上者到“甲车间”工作;180分以下者到“乙车间”工作.查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com