
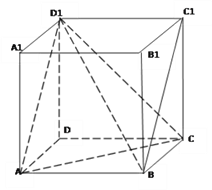
【题目】如图在正方体中![]() 中,
中,
(1)求异面直线![]() 所成的角;
所成的角;
(2)求直线D1B与底面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 大小的正切值.
大小的正切值.
【答案】(1) ![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】试题分析:(1)连接AC,AD1,∠AD1C即为BC1与CD1所成角;
(2)DD1⊥平面ABCD,∠D1DB为直线D1B与平面ABCD所成的角;
(3)连接BD交AC于O,则DO⊥AC,∠D1OD为二面角D1﹣AC﹣D的平面角.
试题解析:
(1)连接AC,AD1,如图所示:

∵BC1∥AD1,
∴∠AD1C即为BC1与CD1所成角,
∵△AD1C为等边三角形,
∴∠AD1C=60°,
故异面直线BC1与CD1所成的角为60°;
(2)∵DD1⊥平面ABCD,
∴∠D1DB为直线D1B与平面ABCD所成的角,
在Rt△D1DB中,sin∠D1DB=![]() =
=![]()
∴直线D1B与平面ABCD所成角的正弦值为![]() ;
;
(3)连接BD交AC于O,则DO⊥AC,
根据正方体的性质,D1D⊥面AC,
∴D1D⊥AC,D1D∩DO=D,
∴AC⊥面D1OD,∴AC⊥D1O,
∴∠D1OD为二面角D1﹣AC﹣D的平面角.
设正方体棱长为1,
在直角三角形D1OD中,DO=![]() ,DD1=1,
,DD1=1,
∴tan∠D1OD=![]() .
.


科目:高中数学 来源: 题型:
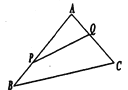
【题目】如图,某生态园将一三角形地块![]() 的一角
的一角![]() 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角![]() 为
为![]() ,
,![]() 的长度均大于
的长度均大于![]() 米,现在边界
米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 总 长度为
总 长度为![]() 米,如何围可使得三角形地块
米,如何围可使得三角形地块![]() 的面积最大?
的面积最大?
(2)已知![]() 段围墙高
段围墙高![]() 米,
米,![]() 段围墙高
段围墙高![]() 米,造价均为每平方米
米,造价均为每平方米![]() 元.若围围墙用了
元.若围围墙用了![]() 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
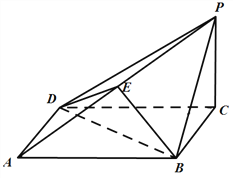
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,点
为正方形,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ) 设![]() ,试判断平面
,试判断平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,写出
能否成立;若成立,写出![]() 的一个值(只需写出结论).
的一个值(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是
A. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点;
内的任意一条直线都没有公共点;
B. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都平行;
内的任意一条直线都平行;
C. 若直线![]() 上有无数个点不在平面
上有无数个点不在平面 ![]() 内,则
内,则![]() ;
;
D. 如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A,B,C的对边分别是a,b,c,且b(sinB-sinC)+(c-a)(sinA+sinC)=0.
(Ⅰ)求角A的大小;
(Ⅱ)若![]() ,
,![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com