根据下面的要求.求S=1+2+22+23+-+263值．(Ⅰ)请完成执行该问题的程序框图(图1),(Ⅱ)图2是解决该问题的程序.请完成执行该问题的程序．题目和参考答案——青夏教育精英家教网—

20．根据下面的要求，求S=1+2+2²+2³+…+2⁶³值．
（Ⅰ）请完成执行该问题的程序框图（图1）；
（Ⅱ）图2是解决该问题的程序，请完成执行该问题的程序．

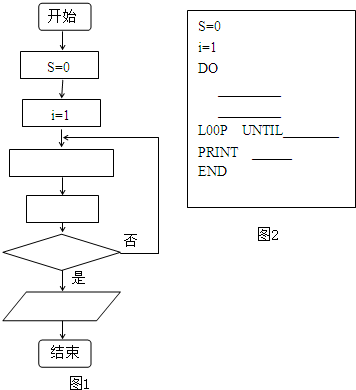
分析（1）分析题目中的要求，发现这是一个累加型的问题，故可能用循环结构来实现，在编写算法的过程中要注意，累加的初始值为0，累加值每一次增加1，退出循环的条件是i＞63，把握住以上要点不难得到正确的流程图．
（2）根据流程图利用DO L00P UNTIL语句可完成执行该问题的完整程序．

解答解：（1）说明：每一个空（1分）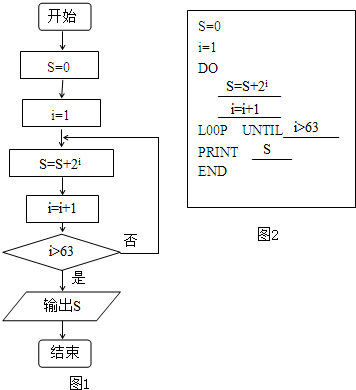

点评可利用循环语句来实现数值的累加（乘）常分如下步骤：①观察S的表达式分析，循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值，累加器的初值为0，累乘器的初值为1，环变量的初值同累加（乘）第一项的相关初值④在循环体中要先计算累加（乘）值，如果累加（乘）值比较简单可以省略此步，累加（乘），给循环变量加步长⑤输出累加（乘）值．

练习册系列答案

英语阅读系列答案

课堂导学案系列答案

中考新航标初中重点知识总复习指导系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

20．已知等差数列3，7，11，15，19，…，则通项公式a_n=4n-1．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．若一位学生把英语单词“error”中字母的拼写错了，则可能出现错误的种数是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．函数f（x）在[a，b]上有定义，若对任意x₁，x₂∈[a，b]，有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{1}{2}[f（{x_1}）+f（{x_2}）]$，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
①f（x）在[1，3]上的图象是连续不断的；
②f（x²）在$[1，\;\sqrt{3}]$上具有性质P；
③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
④任意x₁，x₂，x₃，x₄∈[1，3]，有$f（\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}）≤\frac{1}{4}[f（{x_1}）+f（{x_2}）+f（{x_3}）+f（{x_4}）]$．
其中真命题的序号是（　　）

A．

①②

B．

①③

C．

②④

D．

③④

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的焦点坐标为（　　）

A．

（±$\sqrt{7}$，0）

B．

（0，±$\sqrt{7}$）

C．

（±5，0）

D．

（0，±5）

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．记集合T={0，1，2，3，4，5，6，7，8，9}，$M=\{\frac{a_1}{10}+\frac{a_2}{{{{10}^2}}}+\frac{a_3}{{{{10}^3}}}+\frac{a_4}{{{{10}^4}}}|{a_i}∈T，i=1，2，3，4\}$，将M中的元素按从大到小排列，则第2012个数是（　　）

	A．	$\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{3}{{{{10}^4}}}$		B．	$\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{2}{{{{10}^4}}}$
	C．	$\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{8}{{{{10}^3}}}+\frac{8}{{{{10}^4}}}$		D．	$\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{9}{{{{10}^3}}}+\frac{1}{{{{10}^4}}}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．设数列{a_n}的前n项和S由如下程序框图给出，若输入n的值为100，求输出的S．