
已知 ,
, ,
, 分别为
分别为 三个内角
三个内角 ,
, ,
, 的对边,
的对边,  =
=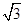
 sin
sin
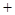
 cos
cos .
.
(1)求角 ;
;
(2)若 =
=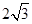 ,
, 的面积为
的面积为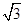 ,求
,求 的周长.
的周长.
(1) 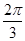 ;(2)
;(2) 
解析试题分析:(1) 根据正弦定理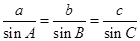 可将
可将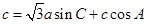 变形为
变形为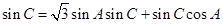 。因为角
。因为角 三角形的内角,所以
三角形的内角,所以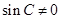 ,可将上式变形为
,可将上式变形为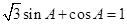 。用化一公式即两角和差公式的逆用将上式左边化简可得
。用化一公式即两角和差公式的逆用将上式左边化简可得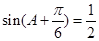 ,根据整体角
,根据整体角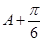 的范围可得
的范围可得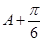 的值,即可得角
的值,即可得角 的值。 (2)由三角形面积
的值。 (2)由三角形面积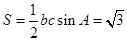 可得
可得 。再结合余弦定理可得
。再结合余弦定理可得 的值,解方程组可得
的值,解方程组可得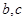 的值,从而可得三角形的周长。
的值,从而可得三角形的周长。
解(1)由 =
=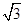
 sin
sin
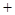
 cos
cos 及正弦定理得
及正弦定理得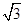 sin
sin sin
sin +cos
+cos sin
sin -sin
-sin =0,
=0,
由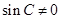 ,所以
,所以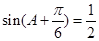 , 4分
, 4分
又0< <π,
<π,
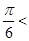
 +
+
 5分
5分
故 =
=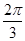 . 6分
. 6分
(2)△ABC的面积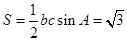 ,故
,故 . 8
. 8
由余弦定理知 2=
2= 2+
2+ 2-2
2-2
 cos
cos ,得
,得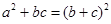
代入 =
=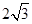 ,
,
 =4解得
=4解得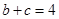 ,故三角形周长为
,故三角形周长为 .(解出
.(解出 ,
, 的值亦可)――12
的值亦可)――12
考点:1正弦定理;2三角形面积公式;3余弦定理。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
(2011•浙江)在△ABC中,角A,B,C,所对的边分别为a,b,c.已知sinA+sinC=psinB(p∈R).且ac= b2.
b2.
(1)当p= ,b=1时,求a,c的值;
,b=1时,求a,c的值;
(2)若角B为锐角,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=a·b,其中向量
 ,向量
,向量
 .
.
(1)求f(x)的最小正周期;
(2)在∆ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a= ,b+c=3,求b,c的长.
,b+c=3,求b,c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•湖北)在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5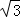 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com