
分析 根据题意,利用等比数列的前n项和公式求出通项公式an,进一步求出数列对应的前n项和公式,再计算$\frac{3}{34}$S12的值.
解答 解:∵anSn+1-an+1Sn+an-an+1=$\frac{1}{2}$anan+1,且Sn+1=Sn+an+1,
∴(an-an+1)Sn+$\frac{1}{2}$anan+1+an-an+1=0,
∴Sn+$\frac{{{a}_{n}a}_{n+1}}{2{(a}_{n}{-a}_{n+1})}$+1=0;
又∵a1=1,令n=1,则1+$\frac{{a}_{2}}{2(1{-a}_{2})}$+1=0,解得a2=$\frac{4}{3}$,
同理可得a3=$\frac{5}{3}$,
猜想an=$\frac{n+2}{3}$;
下面利用数学归纳法证明:
①当n=1时,a1=$\frac{1+2}{3}$=1,成立;
②假设当n≤k(k∈N*)时成立,ak=$\frac{k+2}{3}$,则Sk=$\frac{k(1+\frac{k+2}{3})}{2}$=$\frac{k(k+5)}{6}$;
∵Sk+$\frac{{{a}_{k}a}_{k+1}}{2{(a}_{k}{-a}_{k+1})}$+1=0,
∴$\frac{k(k+5)}{6}$+$\frac{\frac{k+2}{3}{•a}_{k+1}}{\frac{k+2}{3}{-a}_{k+1}}$+1=0,
解得ak+1=$\frac{k+3}{3}$;
因此当n=k+1时也成立,
综上,对于n∈N*,an=$\frac{n+2}{3}$都成立;
由等差数列的前n项和公式得,Sn=$\frac{n(n+5)}{6}$;
∴$\frac{3}{34}$S12=$\frac{3}{34}$×$\frac{12×(12+5)}{6}$=3.
点评 本题考查了等比数列的通项公式与前n项和公式、递推关系、数学归纳法的应用问题,也考查了猜想归纳推理能力与计算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
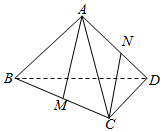 空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )
空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{57}$ | B. | $\sqrt{61}$ | C. | $\sqrt{78}$ | D. | $\sqrt{85}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com