
| A. | A?B | B. | B?A | ||
| C. | A=B | D. | A 与 B 关系不确定 |
分析 将集合A、B中的表达式分别提取$\frac{1}{4}$,再分析得到式子的形式,不难得到B是A的真子集.
解答 解:对于B,x=$\frac{k}{2}$+$\frac{1}{4}$=$\frac{1}{4}$(2k+1),因为k是整数,所以集合A表示的数是$\frac{1}{4}$的奇数倍;
对于A,x=$\frac{k}{4}$+$\frac{1}{2}$=$\frac{1}{4}$(k+2),因为k+2是整数,所以集合B表示的数是$\frac{1}{4}$的整数倍.
因此,集合B的元素必定是集合A的元素,集合A的元素不一定是集合B的元素,即B?A.
故选B.
点评 本题以两个数集为例,叫我们寻找两个集合的包含关系,着重考查了集合的定义与表示和集合包含关系等知识,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
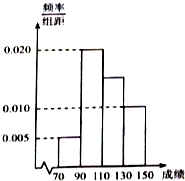 某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.
某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],已知成绩大于等于90分的人数为36人,现采用分层抽样的方式抽取一个容量为10的样本.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知圆内接四边形ABCD,记T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$.
如图所示,已知圆内接四边形ABCD,记T=tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$+tan$\frac{D}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x∈[0,$\frac{π}{2}$],sinx+cosx≥2 | B. | 任意x∈(3,+∞),x2>3x-1 | ||
| C. | 存在x∈R,x2+x=-1 | D. | 任意x∈($\frac{π}{2}$,π),tanx>sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
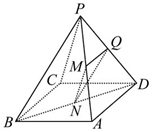 如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com