
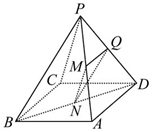
 如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,分析 (1)利用底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,连接AC,可得MN是三角形ACP的中位线,可得MN∥PC.
(2)面面平行转化为线线平行,证明一个平面内的两天直线分别平行另一个平面,并且这两条直线要相交,求利用三角形ADP的中位线MQ∥PB,MN∥PC,可得平面MNQ∥平面PBC.
解答 解:(1)由题意:P-ABCD是四棱锥,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,连接AC,∴N是AC的中点.
∴MN是三角形ACP的中位线,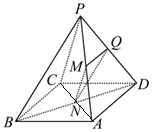
∴MN∥PC.
(2)由(1)可得MN∥PC.
∵M,Q分别在PA,PD的中点上,
∴MQ是三角形ADP的中位线,
∴MQ∥PB.
由MQ∥PB,MN∥PC,PB?平面PBC,PC?平面PBC,PB∩PC=P,
同理MQ?平面MNQ,MN?平面MNQ,MQ∩MN=M.
∴平面MNQ∥平面PBC.
点评 本题考察了线线平行和面面平行的证明,利用了三角形的中位线这性质.比较基础题.


科目:高中数学 来源: 题型:选择题
| A. | 当x>0时,y随x的增大而增大 | B. | 当x=2时,y有最大值-3 | ||
| C. | 图象的顶点坐标为(-2,-7) | D. | 图象与x轴有两个交点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | B?A | ||
| C. | A=B | D. | A 与 B 关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {b} | B. | {d} | C. | {a,c} | D. | {b,d} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com