
分析 由正弦定理及同角三角函数的基本关系判断①;由不等式的性质判断②;举例说明③错误;由已知结合等差数列的通项公式及前n项和推出S2017>1判断④.
解答 解:①,△ABC中角A,B,C的对边分别是a,b,c,若a>b,由正弦定理得sinA>sinB,利用同角三角函数的基本关系可得cosA<cosB,
由sinA>sinB>0,得sin2A>sin2B,∴1-2sin2A<1-2sin2B,则cos2A<cos2B,故①正确;
②,a,b∈R,若a>b,由不等式的性质得a3>b3,故②正确;
③,取a=1,b=3,x=1,满足a<b,$\frac{b}{a}$>$\frac{b+x}{a+x}$,故③错误;
④,等差数列{an}的前n项和为Sn,若S2016-S1=1,则a2+a3+…+a2016=1,
∴2015a1+(d+2d+…+2015d)=1,则$2015{a}_{1}+\frac{(d+2015d)×2015}{2}=1$,
∴${a}_{1}+1008d=\frac{1}{2015}$,即${a}_{1009}=\frac{1}{2015}$,则S2017=2017${a}_{2019}=2017×\frac{1}{2015}$>1,故④正确.
∴正确命题的个数是①②④.
故答案为:①②④.
点评 本题考查命题的真假判断与应用,考查了三角形中的边角关系,训练了等差数列通项公式及前n项和的应用,是中档题.


科目:高中数学 来源: 题型:解答题
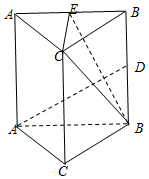 如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.
如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1a2>0,dS3>0 | B. | a1a2<0,dS3>0 | C. | a1a2>0,dS3<0 | D. | a1a2<0,dS3<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com