
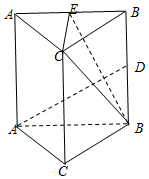
 如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.
如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.分析 (Ⅰ)证明C1E⊥A1B1.C1E⊥AD.AD⊥BE.然后证明AD⊥平面BEC1.
(Ⅱ)取C1C的中点F,连结DF,AF.说明∠ADF为异面直线AD与BC所成的角,在△ADF中,由余弦定理,解得a的值.
解答 解:(Ⅰ)因为三棱柱是直棱柱,
所以平面A1B1C1⊥平面A1B1BA.
因为A1C1=B1C1,E为A1B1的中点,
所以C1E⊥A1B1.
所以C1E⊥平面A1B1BA.
因为AD?平面A1B1BA,
所以C1E⊥AD.
因为A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点,
所以AD⊥BE.
因为C1E?平面BEC1,BE?平面BEC1,C1E∩BE=E,
所以AD⊥平面BEC1.…(6分)
(Ⅱ)取C1C的中点F,连结DF,AF.
因为DF∥BC,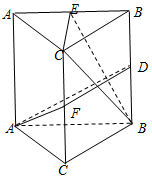
所以∠ADF为异面直线AD与BC所成的角,即∠ADF=60°.
在Rt△ABD中,AB=2,BD=1,
所以$AD=\sqrt{5}$.
在Rt△AFC中,AC=a,CF=1,
所以$AF=\sqrt{{a^2}+1}$.
显然DF=BC=a.
在△ADF中,由余弦定理,得$cos∠ADF=\frac{{A{D^2}+D{F^2}-A{F^2}}}{2AD•DF}$.
所以$\frac{1}{2}=\frac{{5+{a^2}-({a^2}+1)}}{{2\sqrt{5}•a}}$,解得$a=\frac{{4\sqrt{5}}}{5}$.…(13分)
点评 本题考查异面直线所成角,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
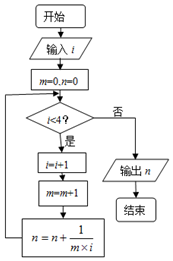
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{-\frac{1}{3}}}$ | C. | $y={x^{\frac{3}{2}}}$ | D. | $y={x^{-\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com