
分析 (1)直接利用集合与集合之间的关系,分类讨论参数a写出不等式,求出a的取值范围;
(2)由题意列出等式,得到f(-x)=f(x)且f(x)≥0成立,从而求出a的值.
解答 解:(1)若关于x的不等式f(x)<0的解集A≠Φ,则△>0,即a≠0;
当a>0时.不等式解集A为(-a,2a);
由题意可知:$\left\{\begin{array}{l}-a≤-1\\ 2a≥2\end{array}\right.$∴a≥1;
当a<0时,不等式解集A为(2a,-a);
由题意可知:$\left\{\begin{array}{l}2a≤-1\\-a≥2\end{array}\right.$∴a≤-2;
综上所述:a∈(-∞,-2]∪[1,+∞);
(2)∵$\left\{\begin{array}{l}f(|x|)-f(x)=0\\|f(x)|-f(x)=0\end{array}\right.$⇒$\left\{\begin{array}{l}{f(-x)=f(x)}\\{f(x)≥0}\end{array}\right.$;
所以有:$\left\{\begin{array}{l}{(-x)^{2}-2a(-x)-2{a}^{2}={x}^{2}-2ax-2{a}^{2}}\\{△≤0}\end{array}\right.$;
解得:$\left\{\begin{array}{l}{a=0}\\{a≤0}\end{array}\right.$⇒a=0;
证明:当a=0时,f(x)=x2 ∴f(|x|)-f(x)=|x|2-x2=0;
又∵|f(x)|-f(x)=|x2|-x2=0;
所以:当a=0时,条件成立.
点评 本题主要考查了集合与不等式基础知识点,以及一元二次函数的性质与存在性命题证明,属中等题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{13}{4}$ | C. | 26 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,1) | B. | (-$\frac{1}{3}$,1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
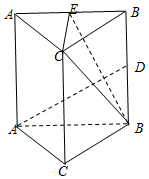 如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.
如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com