
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{-\frac{1}{3}}}$ | C. | $y={x^{\frac{3}{2}}}$ | D. | $y={x^{-\frac{2}{3}}}$ |
分析 根据函数的奇偶性和函数的单调性分别判断即可.
解答 解:对于A:y=${x}^{\frac{2}{3}}$=$\root{3}{{x}^{2}}$,是偶函数,递增,不合题意;
对于B:y=${x}^{-\frac{1}{3}}$=$\frac{1}{\root{3}{x}}$,是奇函数,不合题意;
对于C:函数在(0,+∞)递增,不合题意;
对于D:y=${x}^{-\frac{2}{3}}$=$\frac{1}{\root{3}{{x}^{2}}}$是偶函数,在(0,+∞)递减,符合题意;
故选:D.
点评 本题考查的知识点是函数的单调性的判断与证明,函数奇偶性的判断,是一道基础题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,1) | B. | (-$\frac{1}{3}$,1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
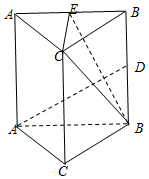 如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.
如图,在直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1中,A1C1=B1C1=a,A1B1=A1A=2,点D,E分别为棱B1B,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
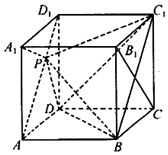 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | [-1,1) | C. | (1,+∞) | D. | [-1,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
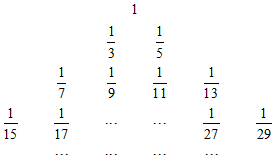
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com