
分析 因为f(x)是R上的增函数,所以若f(x)-3x不是常数,则f[f(x)-3x]便不是常数.而已知f[f(x)-3x]=4,所以f(x)-3x是常数,设f(x)-3x=m,所以f(m)=4,f(x)=3x+m,所以f(m)=3m+m=4,容易知道该方程有唯一解,m=1,所以f(x)=3x+1,所以便可求出f(log35).
解答 解:根据题意得,f(x)-3x为常数,设f(x)-3x=m,则f(m)=4,f(x)=3x+m;
∴3m+m=4,易知该方程有唯一解,m=1;
∴f(x)=3x+1;
∴f(log35)=5+1=6.
故答案为:6.
点评 对于单调函数,当自变量的值是变量时,函数值也是变量,考查单调函数零点的情况.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | log${\;}_{\frac{1}{2}}$m>log${\;}_{\frac{1}{2}}$n | B. | log2m>log2n | ||
| C. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | D. | 2m>2n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^2}$ | B. | (log3x)′=$\frac{1}{xln3}$ | C. | (5x)′=5xlog5e | D. | (x2cosx)′=2xsinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 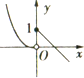 | B. | 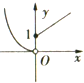 | C. | 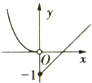 | D. | 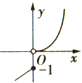 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{10}{69}$ | C. | $\frac{1}{4}$ | D. | $\frac{10}{39}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com