
分析 (1)曲线C恒过定点P(1,0),可得出(t+1)-2(a2+2at)+3at+b=0恒成立,即(1-a)t+1-2a2+b=0恒成立,即可求定值a,b.
(2)求出f(t)=$\frac{2|t|}{{t}^{2}+t+1}$=$\frac{2}{|t+\frac{1}{t}+1|}$.分类讨论,即可得出结论;
(3)由题设知x0是方程(*)的解,x0=1或x0=$\frac{{t}^{2}+3t+1}{{t}^{2}+t+1}$,利用△=(3x0-5)(x0+1)≤0,求x0的取值范围.
解答 解:(1)∵曲线C恒过定点P(1,0),∴(t+1)-2(a2+2at)+3at+b=0恒成立,
即(1-a)t+1-2a2+b=0恒成立,
∴a=1,b=1.
(2)由(1)知曲线C为:(t+1)x2+y2-2(1+2t)x+3t+1=0,
以y=t(x-1)代入得(t2+t+1)x2-2(t+1)2x+t2+3t+1=0(*),
∴x1=1,x2=$\frac{{t}^{2}+3t+1}{{t}^{2}+t+1}$,
∴d=$\sqrt{1+{t}^{2}}|{x}_{1}-{x}_{2}|$=$\frac{2|t|\sqrt{1+{t}^{2}}}{{t}^{2}+t+1}$,
∴f(t)=$\frac{2|t|}{{t}^{2}+t+1}$=$\frac{2}{|t+\frac{1}{t}+1|}$.(t≠0,否则y=0,f(t)=0)
当t>0时,|t+$\frac{1}{t}$+1|=t+$\frac{1}{t}$+1≥3,这时f(t)≤$\frac{2}{3}$;
当t<0时,t+$\frac{1}{t}$≤-2,t+$\frac{1}{t}$+1≤-1,|t+$\frac{1}{t}$+1|≥1,这时f(t)≤2,(t=-1时取等号).
综上讨论:f(t)max=2,这时t=-1.
(3)由题设知x0是方程(*)的解,∴x0=1或x0=$\frac{{t}^{2}+3t+1}{{t}^{2}+t+1}$,
当(x0-1)t2+(x0-3)t+x0-1=0,x2≠1时必须有△=(3x0-5)(x0+1)≤0.
∴x0∈[-1,$\frac{5}{3}$].
点评 本题考查曲线过定点,考查函数的最值,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
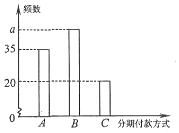 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A,B,C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A,B,C三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元.以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.| 月利润(单位:万元) | 在(0,100]内的部分 | 超过100且不超过150的部分 | 超过150的部分 |
| 税率 | 1% | 2% | 4% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.
已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(2,+∞) | B. | (0,2] | C. | [0,2] | D. | Φ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com