
分析 由$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,n≥2时,问题得以证明.
解答 证明:∵$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,n≥2时,
∴1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)=2-$\frac{1}{n}$.
点评 本题考查了放缩法和裂项求和证明不等式的问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 64π | D. | 128π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 28 | C. | 26 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
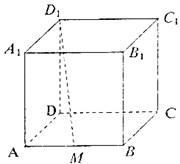 在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,经过点A作D1M的垂面,该垂面被正方体截得部分的面积是( )
在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,经过点A作D1M的垂面,该垂面被正方体截得部分的面积是( )| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com