
分析 (1)运用离心率公式和通径长公式,结合椭圆的a,b,c的关系,解方程即可得到a,b的值,今儿得到椭圆方程;
(2)直线l:y=kx+2与椭圆联立,表示出△AOB面积,利用韦达定理,结合换元,基本不等式,即可求△AOB面积的最大值.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,即a=$\sqrt{3}$c
∵b2=a2-c2=a2-$\frac{1}{3}$a2=$\frac{2}{3}$a2①.
∵MF1⊥x轴
∴|MF1|=$\frac{{b}^{2}}{a}$=$\frac{4\sqrt{3}}{3}$②
由①②可得a=2$\sqrt{3}$,b2=8
∴椭圆的方程为$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1
(2)设A(x1,y1),B(x2,y2),
直线l:y=kx+2与椭圆联立可得(2+3k2)x2+12kx-12=0,
∴x1+x2=-$\frac{12k}{2+3{k}^{2}}$,x1x2=-$\frac{12}{2+3{k}^{2}}$,
又原点到直线l:y=kx+2的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$,
∴△AOB的面积S=$\frac{1}{2}$$\sqrt{1+{k}^{2}}$|x1-x2|d
=|x1-x2|=$\sqrt{\frac{96(1+3{k}^{2})}{(2+3{k}^{2})^{2}}}$,
令t=1+3k2(t≥1),
则S2=$\frac{96t}{1+2t+{t}^{2}}$=$\frac{96}{t+\frac{1}{t}+2}$≤$\frac{96}{2\sqrt{t•\frac{1}{t}}+2}$=24.
当且仅当t=1,即k=0时,△AOB面积的最大值为2$\sqrt{6}$.
点评 本题考查椭圆的方程,考查三角形面积的计算,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
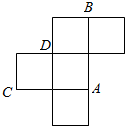 如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{4}{9}$x | C. | y=±$\frac{3}{2}$x | D. | y=±$\frac{9}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 25 | C. | 23 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com