
分析 (I)设点,代入椭圆方程,利用点差法,结合线段PQ的中点为M,再由离心率公式,即可得到结论;
(Ⅱ)由(1)知可得椭圆的方程为2x2+3y2=6c2,设直线l的方程为x=my-5,代入椭圆方程,利用韦达定理及$\overrightarrow{DP}$=2$\overrightarrow{QD}$,确定P,Q坐标之间的关系,表示出面积,利用基本不等式求出S△OPQ的最大值,即可得到椭圆的方程.
解答 解:(I)设P(x1,y1),Q(x2,y2),M(x0,y0),
由题意可得$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
两式相减可得,$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{{a}^{2}}$+$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{{b}^{2}}$=0,
由k1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$,k2=$\frac{{y}_{0}}{{x}_{0}}$=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$,
即有k1k2=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{2}{3}$,
即为2a2=3b2=3(a2-c2),
即c2=$\frac{1}{3}$a2,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$;
(Ⅱ)由(Ⅰ)知,a2=3c2,b2=2c2,
椭圆的方程为2x2+3y2=6c2,①
可设直线l的方程为x=my-5②,
将②代入①中整理得(3+2m2)y2-20my+50-6c2=0,
因为直线l与椭圆交于P,Q两点,所以△=4(12m2c2+18c2-150)>0,
设P(x1,y1),Q(x2,y2),
则y1+y2=$\frac{20m}{3+2{m}^{2}}$,y1y2=$\frac{50-6{c}^{2}}{3+2{m}^{2}}$,
|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{\frac{400{m}^{2}}{(3+2{m}^{2})^{2}}-\frac{200-24{c}^{2}}{3+2{m}^{2}}}$
又$\overrightarrow{DP}$=2$\overrightarrow{QD}$,可得(x1+5,y1)=2(-5-x2,-y2),
即为y1=-2y2,代入韦达定理,可得
c2=$\frac{25+150{m}^{2}}{3+2{m}^{2}}$,
即有|y1-y2|=$\frac{60|m|}{3+2{m}^{2}}$=$\frac{60}{2|m|+\frac{3}{|m|}}$≤$\frac{60}{2\sqrt{6}}$=5$\sqrt{6}$,
当且仅当2|m|=$\frac{3}{|m|}$,即为m=±$\frac{\sqrt{6}}{2}$时,取得等号.
又△0PQ的面积为S=$\frac{1}{2}$|OD|•|y1-y2|=$\frac{5}{2}$|y1-y2|的最大值为$\frac{\sqrt{6}}{2}$,
此时,m2=$\frac{3}{2}$,c2=$\frac{25+225}{6}$=$\frac{125}{3}$,
所求椭圆的方程为2x2+3y2=250,
即$\frac{{x}^{2}}{125}$+$\frac{3{y}^{2}}{250}$=1.
点评 本题考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是确定几何量之间的关系,利用直线与椭圆联立,结合韦达定理和基本不等式求解,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{3}{2}}]$ | B. | $[{-\frac{3}{2},+∞})$ | C. | $[{-4,-\frac{3}{2}}]$ | D. | $[{-\frac{3}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
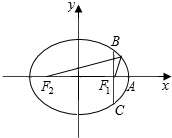 电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.
电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com