
����Ŀ��ij��ҵ����A��Ʒ��������������ָ��ֵ����������ָ��ֵ���ֵȼ�����Ʒ�ۼ����±���
����ָ��ֵm |
|
|
|
��Ʒ�ȼ� | ��Ʒ | ����Ʒ | ����Ʒ |
�ۼۣ�ÿ���� | 160Ԫ | 140Ԫ | 120Ԫ |
�Ӹ���ҵ������A��Ʒ�г�ȡ100����Ϊ���������������ָ��ֵ���õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ.
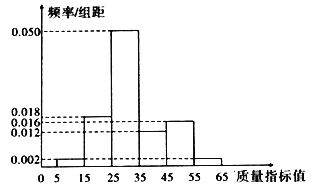
��1������Ƶ�ʷֲ�ֱ��ͼ����A��Ʒ����ָ��ֵ����λ����
��2��������Ƶ�ʹ����������.����һ���˿������������A��Ʒ������֧���ķ���ΪXԪ����X�ķֲ��м���ѧ����.
���𰸡���1��31����2���ֲ��м�������292.
��������
��1��������Ƶ��ֱ��ͼ�У���λ���������ߵ�ֱ��ͼ�������Ƚ�����⼴�ɣ�
��2���������ҵ�����ȡһ��A��ƷΪһ��Ʒ������Ʒ������Ʒ�ĸ��ʣ�Ȼ�����
X�����п���ȡֵ�������ÿ�ֿ��ܵĸ��ʣ�����г��ֲ��м�����ѧ����.
��1����A��������ָ��ֵ����λ��Ϊx����
![]() ����ã�
����ã�![]() .
.
��2��������֪������ҵ�����ȡһ��A��ƷΪһ��Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() ������Ʒ�ĸ���Ϊ
������Ʒ�ĸ���Ϊ![]() .
.
X�����п���ȡֵΪ��240��260��280��300��320.
![]() ��
��![]()
![]()
![]()
����X�ķֲ���Ϊ
X | 240 | 260 | 280 | 300 | 320 |
|
|
|
|
|
|
X����ѧ����![]() ��Ԫ��.
��Ԫ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����Ƴ�һ�����������ֻ���Ϊ�˸��õضԲ�Ʒ������������Ԥ��������ÿ��ֻ��Ƿ��������йأ��������ȡ��50��������й�����Ը���ʾ����飬���÷ֵ���60�֣�˵��������Ը�������÷ֲ�����60�֣�˵��������Ըǿ���������þ�Ҷͼ��ʾ��ͼ��ʾ.

��1�����ݾ�Ҷͼ�е��������![]() �����������ж��Ƿ���95%�İ�����Ϊ�����Ƿ���ÿ��ֻ��������йأ�
�����������ж��Ƿ���95%�İ�����Ϊ�����Ƿ���ÿ��ֻ��������йأ�

��2���ӹ�����Ը���������а�������зֲ����������ȡ5�ˣ�����5���������ȡ2�˽��вɷã�����2�˶����������40��ĸ���.
���� 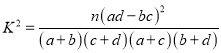 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ������
��������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��������
��������![]() ��
��![]() ǡ��һ��������.
ǡ��һ��������.
(��)������![]() �ļ����귽�̣�
�ļ����귽�̣�
(��)��֪����![]() ������
������![]() ��
��![]() ����
����![]() ����
����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����![]()
![]()
![]() ������
������![]() ����
����![]() ��ǰ
��ǰ![]() ��ͣ�
��ͣ�
��1��������![]() ������Ϊ
������Ϊ![]() .����Ϊ
.����Ϊ![]() �ĵȱ����У�������
�ĵȱ����У�������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��
��![]() ��֤������
��֤������![]() ����
����![]()
![]()
![]() �����
����д��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��3���ڣ�2���������£���![]() ����֤
����֤![]() ������һ���ܿ��Ա�ʾ�ɸ�������������֮��.
������һ���ܿ��Ա�ʾ�ɸ�������������֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��![]() ����ԭ��
����ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ��������Ϊ���ᣬ����������ϵ��ֱ��
��������Ϊ���ᣬ����������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �IJ���������
�IJ���������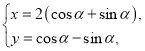 ��
��![]() ��������
��������![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() �Ͼ���Ϊ
�Ͼ���Ϊ![]() �������㣬��
�������㣬��![]() Ϊ����
Ϊ����![]() �ϵĶ����Ҳ���ֱ��
�ϵĶ����Ҳ���ֱ��![]() �ϣ�
�ϣ�
��1��������![]() ����ͨ���̼�ֱ��
����ͨ���̼�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f(x)�Ƕ�����R ������Ϊ1�ĺ�����������![]() �ϣ�
�ϣ� ![]() ���м���D=
���м���D=![]() ����f(x)-lgx=0�Ľ�ĸ�����____________
����f(x)-lgx=0�Ľ�ĸ�����____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ�����³����Ƕ���ڣ�����г����ӵ�ϰ�ߣ������ֳ��ջt���׳������������ų������������Ƕ���ڴ�Ҷ���Ʒ����ʳƷ����˵����Ϊ�˼���ս��ʱ�ڳ�������������ʫ����ԭ.��ͼ��ƽ���ı�����״��ֽƬ���������߳�Ϊ1���������ι��ɵģ����������������������Եõ���ͼ��ʾ������״�������壬�������������Ϊ____����������������һ���������������ֵΪ____��
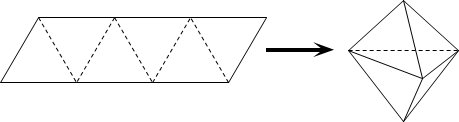
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪˫����
�У���֪˫����![]() ��
��![]() .
.
��1����![]() ��
��![]() ���㣬
���㣬![]() ��
��![]() ��֧��һ��.��
��֧��һ��.��![]() ����
����![]() ������ꣻ
������ꣻ
��2����б��Ϊ1��ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ��Բ
��Բ![]() ���У���֤��
���У���֤��![]() ��
��
��3������Բ![]() ��
��![]() .��
.��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����֤��
����֤��![]() ��ֱ��
��ֱ��![]() �ľ����Ƕ�ֵ.
�ľ����Ƕ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У����߳�a��b��c����a2��a��2b��2c=0��a+2b��2c+3=0����������������ǵĴ�СΪ_____.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com