
某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,又工程丁必须在工程丙完成后立即进行.求安排这6项工程的不同排法种数.
20种
【解析】方法一:设6项工程自左至右占据1~6的6个不同位置.由于工程丙、丁必须相邻且工程丁在工程丙之后,工程丙、丁都在工程甲、乙之后,因此工程丙、丁的位置有以下3类:第一类:工程丙、丁占据3,4位置,则1,2位置分别由工程甲、乙占据,剩余5,6两个位置可由剩余的2项工程占据,共有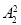 =2种排法;第二类:工程丙、丁占据4,5位置,共有(
=2种排法;第二类:工程丙、丁占据4,5位置,共有(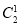 +1)·
+1)·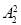 =6种排法;第三类:工程丙、丁占据5,6位置,共有(
=6种排法;第三类:工程丙、丁占据5,6位置,共有( +
+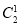 +1)·
+1)·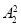 =12种排法.
=12种排法.
由分类加法计数原理,共有2+6+12=20种不同排法.
方法二:由题意,由于丁必须在丙完成后立即进行,故可把丙、丁视为一个大元素,先不管其他限制条件使其与其他四个元素排列共有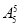 种排法.在所有的这些排法中,考虑甲、乙、丙相对顺序共有
种排法.在所有的这些排法中,考虑甲、乙、丙相对顺序共有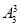 种,故满足条件的排法种数为
种,故满足条件的排法种数为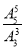 =20种.
=20种.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
从1,2,3,4,5中选3个数,用ξ表示这3个数中最大的一个,则E(ξ)=( )
A.3 B.4.5 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:填空题
从分别写有0,1,2,3,4的五张卡片中取出一张卡片,记下数字后放回,再从中取出一张卡片.则两次取出的卡片上的数字之和恰好等于4的概率是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:填空题
设(2x-1)6=a6x6+a5x5+…+a1x+a0,则|a0|+|a1|+|a2|+…+|a6|=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:解答题
将并排的有不同编号的5个房间安排给5个工作人员临时休息,假定每个人可以选择任一房间,且选择各个房间是等可能的,求恰有2个房间无人选择且这2个房间不相邻的安排方式的种数.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:选择题
在1,2,3,4,5,6这六个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有( )
A.60个 B.36个 C.24个 D.18个
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:填空题
用红、黄、蓝三种颜色去涂图中标号为1、2、…、9的9个小正方形(如图),使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为1、5、9的小正方形涂相同的颜色,则符合条件的所有涂法共有________种.
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:选择题
已知集合A={x|0<ln <1},B={x|
<1},B={x| <x<
<x<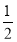 },则A∩B=( )
},则A∩B=( )
A.(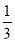 ,
, ) B.∅ C.(
) B.∅ C.(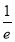 ,
, ) D.(
) D.( ,e)
,e)
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:选择题
在某次数学测试中,学生成绩ξ服从正态分布N(100,σ2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com