
有一批数量很大的环形灯管,其次品率为20%,对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查中止,否则继续抽查,直到抽出次品,但抽查次数最多不超过5次.求抽查次数ξ的分布列.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
用五种不同颜色给图中四个区域涂色,每个区域涂一种颜色.
(1) 共有多少种不同的涂色方法?
(2) 若要求相邻(有公共边)的区域不同色,那么有多少种不同的涂色方法?
| 1 | |
| 2 | |
| 3 | |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2只正品,每次取一个,取出后不放回,直到取出2个正品为止.设X为取出的次数,求X的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为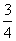 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、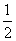 、p2.
、p2.
(1) 求学生甲不能通过A高校自主招生考试的概率;
(2) 设ξ为学生甲在三道程序中获优的次数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是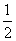 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是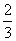 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.
(1) 分别求甲队以3∶0,3∶1,3∶2胜利的概率;
(2) 若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η,且ξ、η分布列为
| ξ | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| η | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(1) 求a、b的值;
(2) 计算ξ、η的期望和方差,并以此分析甲、乙的技术状况.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球.
(1) 若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2) 如果猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com