
甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是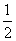 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是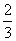 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立.
(1) 分别求甲队以3∶0,3∶1,3∶2胜利的概率;
(2) 若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列.
解:(1) 记“甲队以3∶0胜利”为事件A1,“甲队以3∶1胜利”为事件A2,“甲队以3∶2胜利”为事件A3,由题意,各局比赛结果相互独立,故P(A1)=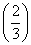
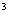 =
=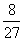 ,
,
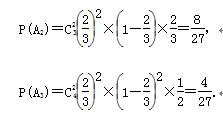 所以,甲队以3∶0、3∶1、3∶2胜利的概率分别是
所以,甲队以3∶0、3∶1、3∶2胜利的概率分别是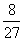 、
、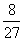 、
、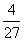 ;
;
(2) 设“乙队以3∶2胜利”为事件A4,由题意,各局比赛结果相互独立,
所以P(A4)=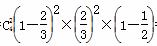 =
=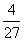 .
.
由题意,随机变量X的所有可能的取值为0,1,2,3,根据事件的互斥性得
P(X=0)=P(A1+A2)=P(A1)+P(A2)=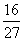 ,
,
P(X=1)=P(A3)=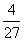 ,
,
P(X=2)=P(A4)=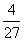 ,
,
P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=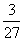 .
.
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P |
|
|
|
|


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
口袋内装有10个相同的球,其中5个球标有数字0,5个球标有数字1.若从袋中摸出5个球,那么摸出的5个球所标数字之和小于2或大于3的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
省工商局于2003年3月份,对全省流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的x饮料的合格率为80%,现有甲、乙、丙3人聚会,选用6瓶x饮料,并限定每人喝2瓶.则甲喝2瓶合格的x饮料的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1) 求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2) 求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3) 记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
有一批数量很大的环形灯管,其次品率为20%,对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查中止,否则继续抽查,直到抽出次品,但抽查次数最多不超过5次.求抽查次数ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知离散型随机变量ξ1的概率分布为
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |
|
|
|
|
|
|
|
离散型随机变量ξ2的概率分布为
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |
|
|
|
|
|
|
|
求这两个随机变量数学期望、方差与标准差.
查看答案和解析>>
科目:高中数学 来源: 题型:
从-1、0、1、2这四个数中选出三个不同的数作为二次函数f(x)=ax2+bx+c的系数组成不同的二次函数,其中使二次函数有两个零点的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com