设两个非零向量a与b不共线．
(1) 若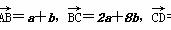
＝3(a－b)．求证：A、B、D三点共线；
(2) 试确定实数k，使ka＋b和a＋kb共线．
优学名师名题系列答案科目：高中数学 来源： 题型：
有一批数量很大的环形灯管，其次品率为20%，对这批产品进行抽查，每次抽出一件，如果抽出次品，则抽查中止，否则继续抽查，直到抽出次品，但抽查次数最多不超过5次．求抽查次数ξ的分布列．
查看答案和解析>>
科目：高中数学 来源： 题型：
下列概率模型：
① 从区间[－5，5]内任取一个数，求取到1的概率；
② 从区间[－5，5]内任取一个数，求取到绝对值不大于1的数的概率；
③ 从区间[－5，5]内任取一个整数，求取到大于1的数的概率；
④ 向一个边长为5 cm的正方形ABCD内投一点P，求点P离中心不超过1 cm的概率．
其中，是几何概型的有__________．(填序号)
查看答案和解析>>
科目：高中数学 来源： 题型：
“抛阶砖”是国外游乐场的典型游戏之一．参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上，抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠)，便可获大奖. 不少人被高额奖金所吸引，纷纷参与此游戏但很少有人得到奖品，请用所学的概率知识解释这是为什么．
分析：在抛阶砖游戏中，首先可以判定此试验为几何概型，我们为了描述每一次随机试验的结果只需要确定金币圆心O的位置即可，一旦圆心位置确定，只要当圆心O到其最近正方形的各边的距离大于其半径时，便可获大奖．由此不难想到一种临界状态，就是当金币与正方形的一边相切时，此时圆心O到该边的距离为1，显然只有当圆心O到最近正方形的各边的距离大于1时才能获奖，所以若中奖，金币圆心必位于小正方形区域A内．
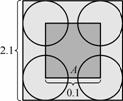
查看答案和解析>>
科目：高中数学 来源： 题型：
某篮球运动员在7天中进行投篮训练的时间(单位：min)用茎叶图表示(如图)，图中左列表示训练时间的十位数，右列表示训练时间的个位数，则该运动员这7天的平均训练时间为________min.
| 6 | 4 | 5 | 7 |
| 7 | 2 | 5 | |
| 8 | 0 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
＝2a＋8b＋3(a－b)＝5(a＋b)＝5
.
共线．
7n－1＋C
7n－2＋…＋C
7被9除的余数是________．
＝2a＋pb，
＝a＋b，
＝a－2b.若A、B、D三点共线，则实数p＝________．
则λ＝________．