Question

如图所示，在△ABC中，∠ACB＝90°，CD⊥AB于D，AE是∠CAB的角平分线，CD与AE相交于点F，EG⊥AB于G．

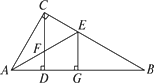
求证：EG²＝FD·EB．

Answer 1

答案：
解析：

证明：因为∠ACE＝90°，CD⊥AB， 　　所以∠CAE＋∠AEC＝90°，∠FAD＋∠AFD＝90°． 　　因为∠AFD＝∠CFE，所以∠FAD＋∠CFE＝90°． 　　又因为∠CAE＝∠FAD， 　　所以∠AEC＝∠CFE．所以CF＝CE． 　　因为AE是∠CAB的平分线，EG⊥AB，EC⊥AC， 　　所以EC＝EG，CF＝EG． 　　因为∠B＋∠CAB＝90°，∠ACF＋∠CAB＝90°， 　　所以∠ACF＝∠B． 　　因为∠CAF＝∠BAE， 　　所以△AFC∽△AEB， 　　因为CD⊥AB，EG⊥AB， 　　所以Rt△ADF∽Rt△AGE． 　　所以＝，＝． 　　所以CF·EG＝FD·EB，EG2＝FD·EB． 　　分析：欲证EG2＝FD·EB，即证＝，易证＝，EG＝CF，故只需证＝，亦即证△AFC∽△AEB．

提示：

对于直角三角形相似的判定，有一种特殊方法是：直角三角形被斜边上的高分成的两个直角三角形与原三角形相似．