练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知数列{an}为等比数列，若a1+a2016=8，则a1（a1+2a2016+a4031）的值为64．

    分析 由等比数列的通项公式推导出a1（a1+2a2016+a4031）=${{a}_{1}}^{2}+2{a}_{1}{a}_{2016}+{{a}_{2016}}^{2}$=$（{a}_{1}+{a}_{2016}）^{2}$，由此能求出结果．

    解答 解：∵数列{an}为等比数列，a1+a2016=8，
    ∴a1（a1+2a2016+a4031）
    =${{a}_{1}}^{2}+2{a}_{1}{a}_{2016}+{a}_{1}{a}_{4031}$
    =${{a}_{1}}^{2}+2{a}_{1}{a}_{2016}+{{a}_{2016}}^{2}$
    =$（{a}_{1}+{a}_{2016}）^{2}$
    =82=64．
    故答案为：64．

    点评 本题考查等比数列的代数式的值的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知曲线C1的极坐标方程为ρ=8$\sqrt{2}$cos（θ-$\frac{3π}{4}$），曲线C2的参数方程为$\left\{\begin{array}{l}{x=8cosθ}\\{y=3sinθ}\end{array}\right.$，（θ为参数）．
    （1）将曲线C1的极坐标方程化为直角坐标方程，将曲线C2的参数方程化为普通方程；
    （2）若P是曲线C2上的动点，求P到直线l：$\left\{\begin{array}{l}{x=3+2t}\\{y=-2+t}\end{array}\right.$，（t为参数）的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某校高三文科500名学生参加了3月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从500名学生中抽取100名学生的成绩进行统计分析，抽出的100名学生的地理、历史成绩如表：
    地理
    历史    		[80，100][60，80][40，60]
    [80，100]8m9
    [60，80]9n9
    [40，60]8157
    若历史成绩在[80，100]区间的占30%，
    （1）求m，n的值；
    （2）请根据上面抽出的100名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
    [80，100][60，80][40，60]
    地理
    历史
    根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知椭圆C1：$\frac{x^2}{m+1}$+$\frac{y^2}{3-n}$=1与双曲线C2：$\frac{x^2}{m}$-$\frac{y^2}{-n}$=1有相同的焦点，则双曲线C2的一条斜率为正的渐近线的倾斜角的取值范围为（　　）
    A．（45°，90°）B．（45°，90°]C．（0，45°）D．（45°，60°）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．依次连接正六边形各边的中点，得到一个小正六边形，再依次连接这个小正六边形各边的中点，得到一个更小的正六边形，往原正六边形内随机洒一粒种子，则种子落在最小的正六边形内的概率为（　　）
    A．$\frac{3}{4}$B．$\frac{9}{16}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F1、F2是一对相关曲线的焦点，P是它们在第一象限的交点，当∠F1PF2=30°时，这一对相关曲线中椭圆的离心率是（　　）
    A．7-4$\sqrt{3}$B．2-$\sqrt{3}$C．$\sqrt{3}$-1D．4-2$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

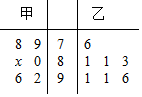    5．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85．
    （Ⅰ） 计算甲班7位学生成绩的方差s2； 
    （Ⅱ）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在平面直角坐标系xOy中，过定点Q（1，1）的直线与曲线y=$\frac{x}{x-1}$交于M，N两点，则$\overrightarrow{OQ}$•$\overrightarrow{OM}$-$\overrightarrow{OQ}$•$\overrightarrow{NO}$=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若实数a，b满足$\frac{4}{a}$+$\frac{1}{b}$=$\sqrt{ab}$，则ab的最小值为4．

    查看答案和解析>>

    同步练习册答案