Question

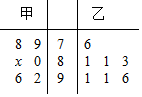
5．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85．
（Ⅰ） 计算甲班7位学生成绩的方差s²； 
（Ⅱ）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．

Answer 1

分析 （Ⅰ）根据平均数和方差 的定义求出即可；
（Ⅱ）求出所有的基本事件的个数，再求出满足条件的基本事件，从而求出其概率．

解答 解：（ I）∵甲班学生的平均分是85，
∴$\frac{92+96+80+80+x+85+79+78}{7}$=85，
∴x=5．
则甲班7位学生成绩的方差为：
s²=$\frac{1}{7}$[36+47+25+0+0+49+121]=40．
（ II）甲班成绩在90（分）以上的学生有两名，分别记为A，B，
乙班成绩在90（分）以上的学生有三名，分别记为C，D，E． 
从这五名学生任意抽取两名学生共有10种情况：
（A，B），（A，C），（A，D），（A，E），（B，C），
（B，D），（B，E），（C，D），（C，E），（D，E）． 
其中甲班至少有一名学生共有7种情况：
（A，B），（A，C），（A，D），（A，E），（B，C），（B，D），（B，E）
记“甲班至少有一名学生”为事件M，
则P（M）=$\frac{7}{10}$，
即从成绩在90（分）以上的学生中随机抽取两名学生，甲校至少有一名学生的概率为$\frac{7}{10}$．

点评 本题考查了茎叶图问题，考查平均数和方差的公式，考查条件概率，是一道中档题．