
| A. | 相离 | B. | 相切 | C. | 相交且过圆心 | D. | 相交但不过圆心 |
分析 把圆的方程及直线的方程化为普通方程,然后利用点到直线的距离公式求出圆心到已知直线的距离d,判定发现d小于圆的半径r,又圆心不在已知直线上,则直线与圆的位置关系为相交但不过圆心.
解答 解:把圆的参数方程化为普通方程得:(x-2)2+(y-1)2=4,
∴圆心坐标为(2,1),半径r=2,
把直线的参数方程化为普通方程得:x-y+1=0,
∴圆心到直线的距离d=$\frac{|2-1+1|}{\sqrt{1+(-1)^{2}}}=\sqrt{2}$<r=2,
又圆心(2,1)不在直线x-y+1=0上,
则直线与圆的位置关系为相交但不过圆心.
故选:D.
点评 本题考查了参数方程与普通方程的互化,及直线与圆的位置关系,其中直线与圆的位置关系为:(d为圆心到直线的距离,r为圆的半径)0≤d<r,直线与圆相交;d=r,直线与圆相切;d>r,直线与圆相离,是基础题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
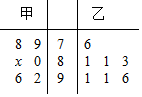 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $-\frac{{2\sqrt{6}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
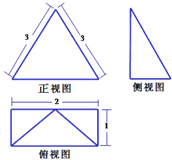 一个空间几何体的三视图如图,其中主视图是腰长为3的等腰三角形,俯视图是边长分别为1,2的矩形,则该几何体的体积等于( )
一个空间几何体的三视图如图,其中主视图是腰长为3的等腰三角形,俯视图是边长分别为1,2的矩形,则该几何体的体积等于( )| A. | 2 | B. | $4\sqrt{2}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(2)<f(4) | B. | f(2)<f(-1)<f(4) | C. | f(2)<f(4)<f(-1) | D. | f(4)<f(2)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | [-1,3] | C. | (-∞,-1]∪[3,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{π}{3}$ | B. | $arcsin\frac{{\sqrt{6}}}{3}$ | C. | $\frac{π}{6}$ | D. | $arcsin\frac{{2\sqrt{39}}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com