练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．函数y=log2（x2-2x-3）的定义域为（　　）
    A．（-∞，-1）∪（3，+∞）B．[-1，3]C．（-∞，-1]∪[3，+∞）D．（-1，3）

    分析 根据函数成立的条件即可求函数的定义域．

    解答 解：要使函数有意义，则x2-2x-3＞0，即x＞3或x＜-1，即函数的定义域为（-∞，-1）∪（3，+∞），
    故选：A．

    点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知集合A={-2，0，2}，B={x|x2-x-2=0}，则∁A（A∩B）=（　　）
    A．{-2，0}B．{2，0}C．{-2，-1，0}D．{2，1，0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．直线l：$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数）与圆C：$\left\{\begin{array}{l}x=2+2cosθ\\ y=1+2sinθ\end{array}\right.$（θ为参数）的位置关系是（　　）
    A．相离B．相切C．相交且过圆心D．相交但不过圆心

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知三梭锥P-ABC中，PA=4，AB=AC=2$\sqrt{3}$，BC=6，PA⊥面ABC，则此三棱锥的外接球的表面积为（　　）
    A．16πB．32πC．64πD．128π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．给出以下命题：
    ①命题“若am2＜bm2”，则“a＜b”的逆命题是真命题；
    ②命题“p或q”为真命题，则命题p和命题q均为真命题；
    ③已知x∈R，则“x＞1”是“x＞2”的充分不必要条件；
    ④命题“?x∈R，x2-x＞0”的否定是：“?x∈R，x2-x≤0”
    其中真命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．各项为正数的数列{an}的前n项和为Sn，且满足：Sn=$\frac{1}{4}$an2+$\frac{1}{2}$an+$\frac{1}{4}$（n∈N*）
    （Ⅰ）求an
    （Ⅱ）设数列{$\frac{1}{a_n^2}$}的前n项和为Tn，证明：对一切正整数n，都有Tn＜$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

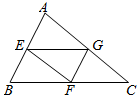    10．如图，在△ABC中，AB=2$\sqrt{5}$，BC=2$\sqrt{10}$，AC=2$\sqrt{13}$，E、F、G分别为三边中点，将△BEF，△AEG，△GCF分别沿EF、EG、GF向上折起，使A、B、C重合，记为S，则三棱锥S-EFG的外接球面积为（　　）
    A．14πB．15πC．$\frac{29}{2}$πD．2$\sqrt{33}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在△ABC中，若sinA=2sinB，cosC=-$\frac{1}{4}$，则$\frac{a}{c}$=（　　）
    A．$\sqrt{6}$B．$\frac{{\sqrt{6}}}{2}$C．$\frac{{\sqrt{6}}}{3}$D．$\frac{{\sqrt{6}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

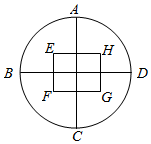    8．如图所示是外框为圆形的一种图标．已知圆的半径为60mm，A，B，C，D是圆周的四等分点，圆内框架总长是360mm，设计要求是：矩形EFGH的周长与面积的比值最小．试问矩形EFGH的长与宽各是多少mm时符合设计要求．此时的比值是多少？

    查看答案和解析>>

    同步练习册答案