
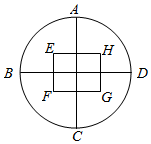
 如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少?
如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少? 分析 设矩形EFGH的长为xmm,宽为ymm,可得周长为2(x+y),面积为xy,由题意可得x+y=60,运用基本不等式可得xy的最大值,进而得到所求最小值及x,y的值.
解答 解:设矩形EFGH的长为xmm,宽为ymm,
周长为2(x+y),面积为xy,
由题意可得2(x+y)=360-4×60=120,
即x+y=60,
则矩形EFGH的周长与面积的比值为$\frac{2(x+y)}{xy}$=$\frac{120}{xy}$,
由xy≤($\frac{x+y}{2}$)2=900,
可得$\frac{120}{xy}$≥$\frac{120}{900}$=$\frac{2}{15}$.
当且仅当x=y=30时,比值最小,且为$\frac{2}{15}$.
即有矩形EFGH的长与宽均为30mm时符合设计要求.
此时的比值是$\frac{2}{15}$.
点评 本题考查数学模型的应用题的解法,注意运用基本不等式,考查运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | [-1,3] | C. | (-∞,-1]∪[3,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{π}{3}$ | B. | $arcsin\frac{{\sqrt{6}}}{3}$ | C. | $\frac{π}{6}$ | D. | $arcsin\frac{{2\sqrt{39}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,1) | B. | (-1,1) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,-1)∪(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$-cos1 | B. | $\frac{10}{3}$-cos1 | C. | $\frac{7}{3}$+cos1 | D. | $\frac{10}{3}$+cos1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com